题目内容
一个口袋中装有2个白球和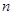 个红球(
个红球( 且
且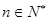 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(Ⅰ) 摸球一次,若中奖概率为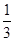 ,求
,求 的值;
的值;
(Ⅱ) 若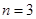 ,摸球三次,记中奖的次数为
,摸球三次,记中奖的次数为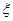 ,试写出
,试写出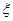 的分布列并求其期望.
的分布列并求其期望.
【答案】
(Ⅰ) 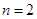 ;(Ⅱ )
;(Ⅱ ) 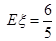 .
.
【解析】
试题分析:(Ⅰ) 由古典概率的求法,可求出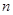 ;(Ⅱ ) 摸球三次,中奖情况可能为;0,1,2,3次,分别求出概率,得分布列从而求出期望.
;(Ⅱ ) 摸球三次,中奖情况可能为;0,1,2,3次,分别求出概率,得分布列从而求出期望.
试题解析:(1)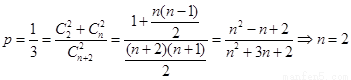 ;
;
(2)若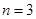 ,则每次摸球中奖的概率
,则每次摸球中奖的概率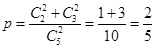
因此,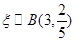 ,分布列如下:
,分布列如下:
|
|
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
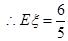 .
.
考点:1、古典概率的求法,2、分布列与期望的求法.

练习册系列答案
相关题目
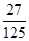
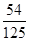

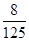
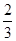 B.
B.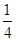 C.
C.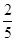 D.
D.