题目内容
已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b= ,A+C=2B,则sinA= .
,A+C=2B,则sinA= .

解析试题分析:在△ABC中,A+C=2B,A+C+B=180°
∴A+C=120°,B=60°
∵a=1,b= ,则由正弦定理
,则由正弦定理 ,可知
,可知 ,故答案为
,故答案为
考点:本题主要考查了三角形的内角和定理及正弦定理在解三角形中的应用,属于基础试题
点评:解决该试题的关键是在△ABC中,A+C=2B,A+C+B=180°可求B,由正弦定理可得sinA的值,进而得到结论。

练习册系列答案
相关题目

 ,则外接圆的半径为___
,则外接圆的半径为___
 部分图象如图所示,
部分图象如图所示, 为图象的最高点,
为图象的最高点, 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形.则
为正三角形.则 = .
= . 
 中,
中, ,
, ,则
,则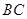 的取值范围是
的取值范围是 .
. ABC中.sin2A
ABC中.sin2A ,.则A的取值范围是
,.则A的取值范围是 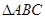 中,如果
中,如果 ,则角B的大小为
,则角B的大小为  中,若
中,若 ,
, ,
,  ,则
,则 .
.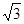 ,则
,则 等于
等于