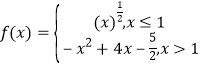Question

【题目】已知函数．

（1）求的单调区间；

（2）求的最大值和最小值．

Answer 1

【答案】（1）见解析；（2）最大值为6，最小值为.

【解析】

（1）求出原函数的导函数，分别利用导函数大于0和小于0，结合已知函数定义域求得原函数的单调区间；

（2）求出函数在[﹣2，1]两端点的值，再求出函数在该区间上的最大值得答案．

（1） f′(x)＝3x2＋4x＋1＝3(x＋)(x＋1)．由f′(x)>0，得x<－1或x>－；

由f′(x)<0，得－1<x<－.因此，函数f(x)在[－，1]上的单调递增区间为[－，－1]，[－，1]，单调递减区间为[－1，－]．

（2）f(x)在x＝－1处取得极大值为f(－1)＝2；

f(x)在x＝－处取得极小值为f(－)＝.

又∵f(－)＝，f(1)＝6，且>，

∴f(x)在[－，1]上的最大值为f(1)＝6，最小值为f.