题目内容
已知直线l经过点P(3,1),且被两平行直线l1;x+y+1=0和l2:x+y+6=0截得的线段之长为5,求直线l的方程.分析:法一如图,若直线l的斜率不存在,直线l的斜率存在,利用点斜式方程,分别与l1、l2联立,求得两交点A、B的坐标(用k表示),再利用|AB|=5可求出k的值,从而求得l的方程.
法二:求出平行线之间的距离,结合|AB|=5,设直线l与直线l1的夹角为θ,求出直线l的倾斜角为0°或90°,然后得到直线方程.就是用l1、l2之间的距离及l与l1夹角的关系求解.
法三:设直线l1、l2与l分别相交于A(x1,y1),B(x2,y2),
则通过求出y1-y2,x1-x2的值确定直线l的斜率(或倾斜角),从而求得直线l的方程.
法二:求出平行线之间的距离,结合|AB|=5,设直线l与直线l1的夹角为θ,求出直线l的倾斜角为0°或90°,然后得到直线方程.就是用l1、l2之间的距离及l与l1夹角的关系求解.
法三:设直线l1、l2与l分别相交于A(x1,y1),B(x2,y2),
则通过求出y1-y2,x1-x2的值确定直线l的斜率(或倾斜角),从而求得直线l的方程.
解答: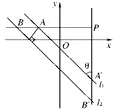 解:解法一:若直线l的斜率不存在,则直线l的方程为x=3,
解:解法一:若直线l的斜率不存在,则直线l的方程为x=3,
此时与l1、l2的交点分别为A′(3,-4)或B′(3,-9),
截得的线段AB的长|AB|=|-4+9|=5,符合题意.
若直线l的斜率存在,则设直线l的方程为y=k(x-3)+1.
解方程组
得
A(
,-
).
解方程组
得
B(
,-
).
由|AB|=5.
得(
-
)2+(-
+
)2=52.
解之,得k=0,直线方程为y=1.
综上可知,所求l的方程为x=3或y=1.
解法二:由题意,直线l1、l2之间的距离为d=
=
,
且直线L被平行直线l1、l2所截得的线段AB的长为5,
设直线l与直线l1的夹角为θ,则sinθ=
=
,故θ=45°.
由直线l1:x+y+1=0的倾斜角为135°,知直线l的倾斜角为0°或90°,
又由直线l过点P(3,1),故直线l的方程为:x=3或y=1.
解法三:设直线l与l1、l2分别相交A(x1,y1)、B(x2,y2),则x1+y1+1=0,x2+y2+6=0.
两式相减,得(x1-x2)+(y1-y2)=5.①
又(x1-x2)2+(y1-y2)2=25.②
联立①、②可得
或
由上可知,直线l的倾斜角分别为0°或90°.
故所求的直线方程为x=3或y=1.
 解:解法一:若直线l的斜率不存在,则直线l的方程为x=3,
解:解法一:若直线l的斜率不存在,则直线l的方程为x=3,此时与l1、l2的交点分别为A′(3,-4)或B′(3,-9),
截得的线段AB的长|AB|=|-4+9|=5,符合题意.
若直线l的斜率存在,则设直线l的方程为y=k(x-3)+1.
解方程组
|
A(
| 3k-2 |
| k+1 |
| 4k-1 |
| k+1 |
解方程组
|
B(
| 3k-7 |
| k+1 |
| 9k-1 |
| k+1 |
由|AB|=5.
得(
| 3k-2 |
| k+1 |
| 3k-7 |
| k+1 |
| 4k-1 |
| k+1 |
| 9k-1 |
| k+1 |
解之,得k=0,直线方程为y=1.
综上可知,所求l的方程为x=3或y=1.
解法二:由题意,直线l1、l2之间的距离为d=
| |1-6| | ||
|
5
| ||
| 2 |
且直线L被平行直线l1、l2所截得的线段AB的长为5,
设直线l与直线l1的夹角为θ,则sinθ=
| ||||
| 5 |
| ||
| 2 |
由直线l1:x+y+1=0的倾斜角为135°,知直线l的倾斜角为0°或90°,
又由直线l过点P(3,1),故直线l的方程为:x=3或y=1.
解法三:设直线l与l1、l2分别相交A(x1,y1)、B(x2,y2),则x1+y1+1=0,x2+y2+6=0.
两式相减,得(x1-x2)+(y1-y2)=5.①
又(x1-x2)2+(y1-y2)2=25.②
联立①、②可得
|
|
由上可知,直线l的倾斜角分别为0°或90°.
故所求的直线方程为x=3或y=1.
点评:本题是中档题,考查直线与直线的位置关系,直线与直线所成的角,直线的点斜式方程,斜率是否存在是容易出错的地方,注意本题的三种方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,
A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,