题目内容
求下列数列的一个通项公式:
⑴
⑵
⑶
⑷
⑴

⑵

⑶

⑷

⑴ ⑵
⑵ ⑶
⑶ ⑷
⑷
 ⑵
⑵ ⑶
⑶ ⑷
⑷
⑴联想数列 即数列
即数列 ,可得数列的通项公式
,可得数列的通项公式 ;
;
⑵将原数列改写为 分母分别为
分母分别为 分子分别为
分子分别为
 呈周期性变化,可以用
呈周期性变化,可以用 ,或
,或 ,或
,或 表示.
表示.
 (或
(或 ,或
,或 )
)
⑶分子为正偶数列,分母为 得
得 
⑷观察数列可知:

本题也可以利用关系式 求解.
求解.
【名师指引】⑴联想和转换是由已知认识未知的两种有效的思维方法.
⑵求数列的通项公式,应运用观察、分析、归纳、验证的方法.易错之处在于每个数列由前几项找规律不准确,以及观察、分析、归纳、验证这四个环节做的不够多,应注意对每一数列认真找出规律和验证.
 即数列
即数列 ,可得数列的通项公式
,可得数列的通项公式 ;
;⑵将原数列改写为
 分母分别为
分母分别为 分子分别为
分子分别为 呈周期性变化,可以用
呈周期性变化,可以用 ,或
,或 ,或
,或 表示.
表示. (或
(或 ,或
,或 )
)⑶分子为正偶数列,分母为
 得
得 
⑷观察数列可知:


本题也可以利用关系式
 求解.
求解. 【名师指引】⑴联想和转换是由已知认识未知的两种有效的思维方法.
⑵求数列的通项公式,应运用观察、分析、归纳、验证的方法.易错之处在于每个数列由前几项找规律不准确,以及观察、分析、归纳、验证这四个环节做的不够多,应注意对每一数列认真找出规律和验证.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 (
( ),及
),及 ,求
,求
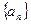 中,
中,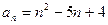 .
.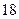 是数列中的第几项?
是数列中的第几项?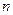 为何值时,
为何值时,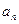 有最小值?并求最小值.
有最小值?并求最小值. 的前
的前 项和
项和 ,则此数列的通项公式为 .
,则此数列的通项公式为 . 满足:
满足: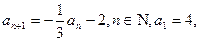 求
求
 中,
中, ,
, ,则
,则 的值是( )
的值是( )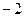


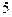
 ,的通项公式的是 。
,的通项公式的是 。 ,则
,则 =___ _______.
=___ _______.