题目内容
已知f(x)是R上的偶函数,当x≥0时,f (x)=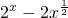 ,又a是函数g (x)=
,又a是函数g (x)=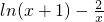 的正零点,则f(-2),f(a),f(1.5)的大上关系是
的正零点,则f(-2),f(a),f(1.5)的大上关系是
- A.f(1.5)<f(a)<f(-2)
- B.f(-2)<f(1.5)<f(a)
- C.f(a)<f(1.5)<f(-2)
- D.f(1.5)<f(-2)<f(a)
A
分析:本题考查的是函数的单调性与奇偶性的综合类问题.在解答时可先结合零点定理获得a与1.5和2的关系:1.5<a<2,然后利用求导获得函数f(x)的单调性,再有单调性即可获得问题的解答.
解答:当a>0时,易知g(x)为增函数,而且g(2)=ln3-1>0,g(1.5)=ln2.5- <lne-1=0,于是由零点存在定理可知在区间(1.5,2)内g(x)存在零点,再由单调性结合题意可知a就为这个零点,因此有1.5<a<2.又当x≥0时,直接求导即得
<lne-1=0,于是由零点存在定理可知在区间(1.5,2)内g(x)存在零点,再由单调性结合题意可知a就为这个零点,因此有1.5<a<2.又当x≥0时,直接求导即得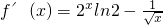 ,于是当x>1时,我们有f'(x)>2ln2-1=ln22-1>lne-1=0,由此可见f(x)在(1,+∞)上单调增,可见必有f(1.5)<f(a)<f(2),而又由于f(x)为偶函数,所以f(1.5)<f(a)<f(-2).
,于是当x>1时,我们有f'(x)>2ln2-1=ln22-1>lne-1=0,由此可见f(x)在(1,+∞)上单调增,可见必有f(1.5)<f(a)<f(2),而又由于f(x)为偶函数,所以f(1.5)<f(a)<f(-2).
故选A.
点评:本题考查的是函数的单调性与奇偶性的综合类问题.在解答时充分体现了零点定理、导数知识的灵活应用.其中数形结合的思想、问题转化的思想在题目中也得到了充分的展现.值得同学们体会和反思.
分析:本题考查的是函数的单调性与奇偶性的综合类问题.在解答时可先结合零点定理获得a与1.5和2的关系:1.5<a<2,然后利用求导获得函数f(x)的单调性,再有单调性即可获得问题的解答.
解答:当a>0时,易知g(x)为增函数,而且g(2)=ln3-1>0,g(1.5)=ln2.5-
 <lne-1=0,于是由零点存在定理可知在区间(1.5,2)内g(x)存在零点,再由单调性结合题意可知a就为这个零点,因此有1.5<a<2.又当x≥0时,直接求导即得
<lne-1=0,于是由零点存在定理可知在区间(1.5,2)内g(x)存在零点,再由单调性结合题意可知a就为这个零点,因此有1.5<a<2.又当x≥0时,直接求导即得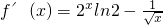 ,于是当x>1时,我们有f'(x)>2ln2-1=ln22-1>lne-1=0,由此可见f(x)在(1,+∞)上单调增,可见必有f(1.5)<f(a)<f(2),而又由于f(x)为偶函数,所以f(1.5)<f(a)<f(-2).
,于是当x>1时,我们有f'(x)>2ln2-1=ln22-1>lne-1=0,由此可见f(x)在(1,+∞)上单调增,可见必有f(1.5)<f(a)<f(2),而又由于f(x)为偶函数,所以f(1.5)<f(a)<f(-2).故选A.
点评:本题考查的是函数的单调性与奇偶性的综合类问题.在解答时充分体现了零点定理、导数知识的灵活应用.其中数形结合的思想、问题转化的思想在题目中也得到了充分的展现.值得同学们体会和反思.

练习册系列答案
相关题目