题目内容
下表给出了从某校500名12岁男生中用简单随机抽样得出的120人的身高资料(单位:厘米):
(1)在这个问题中,总体是什么?并求出x与y的值;
(2)求表中x与y的值,画出频率分布直方图及频率分布折线图;
(3)试计算身高在146~154cm的总人数约有多少?
| 分组 | 人数 | 频率 |
| [122,126) | 5 | 0.042 |
| [126,130) | 8 | 0.067 |
| [130,134 ) | 10 | 0.083 |
| [134,138) | 22 | 0.183 |
| [138,142) | | y |
| [142,146) | 20 | 0.167 |
| [146,150) | 11 | 0.092 |
| [150,154) | x | 0.050 |
| [154,158) | 5 | 0.042 |
| 合计 | 120 | 1.00 |
(1)在这个问题中,总体是什么?并求出x与y的值;
(2)求表中x与y的值,画出频率分布直方图及频率分布折线图;
(3)试计算身高在146~154cm的总人数约有多少?
(1)详见解析;(2)详见解析;(3)71.
试题分析:(1)根据数据总体的定义及已知中从某校500名12岁男生中用简单随机抽样得出的120人的身高资料进行调查,我们易得到结论;(2)根据各组的频率和为1,及频率=频数÷样本容量,可计算出x,y的值.(3)根据146~154cm范围内各组的频率和,根据频数=频率×总体容量,即可估计出身高在146~154cm的总人数约有多少.
解:(1)本题中的总体是指某校500名12岁男生的身高;身高分布在[150,154)的学生有x人,在样本120人占的频率为0.050;所以:x=120
 0.050="6;" 身高分布在[138,142)的学生占的频率y=1-(0.042+0.067+0.083+0.183+0.167+0.092+0.050+0.042)=0.274;
0.050="6;" 身高分布在[138,142)的学生占的频率y=1-(0.042+0.067+0.083+0.183+0.167+0.092+0.050+0.042)=0.274;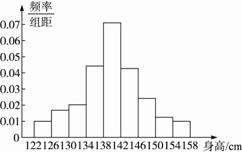
(2)样本的频率分布直方图及频率分布折线图如上所示;
(3)因为样本中身高在146~154cm的频率为0.092+0.050=0.142,以此来估计总体中身高在146~154cm的概率大约为0.142,从而估计身高在146~154cm的总人数约为500
 0.142=71.
0.142=71.
练习册系列答案
相关题目

 ,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共抽取100件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为
,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共抽取100件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为 ,则抽取的100件产品的使用寿命的平均值为_______
,则抽取的100件产品的使用寿命的平均值为_______ .
.