题目内容
关于平面向量有下列四个命题:①若
| a |
| b |
| a |
| c |
| b |
| c |
②已知
| a |
| b |
| a |
| b |
③非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
④(
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
其中正确的命题为
分析:通过举反例知①不成立,由平行向量的坐标对应成比列知②正确,由向量加减法的意义知,③正确,通过化简计算得④正确.
解答:解:当
=
时,可得到①不成立.
对于②
∥
时,有
=
,∴k=-1,故②正确.
当|
|=|
|=|
-
|时,
、
、
-
这三个向量平移后构成一个等边三角形,
+
是这个等边三角形一条角平分线,故③正确.
∵(
+
)•(
-
)=(
)2-(
)2=1-1=0,故④正确.
综上,②③④正确,①不正确,
故答案为 ②③④.
| a |
| 0 |
对于②
| a |
| b |
| k |
| -2 |
| 3 |
| 6 |
当|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∵(
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| a | ||
|
|
| ||
|
综上,②③④正确,①不正确,
故答案为 ②③④.
点评:本题考查两个向量的数量积公式,两个向量加减法的几何意义,以及共线向量的坐标特点.

练习册系列答案
相关题目
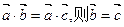 ;②已知
;②已知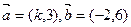 .若
.若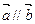 ,则
,则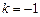 ;③非零向量
;③非零向量 ,满足
,满足 ,则
,则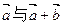 的夹角为
的夹角为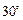 ;④
;④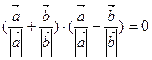 .其中正确的命题为___________.(写出所有正确命题的序号)
.其中正确的命题为___________.(写出所有正确命题的序号)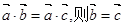 ;②已知
;②已知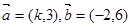 .若
.若 ,则
,则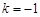 ;③非零向量
;③非零向量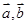 ,满足
,满足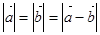 ,则
,则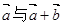 的夹角为
的夹角为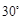 ;④
;④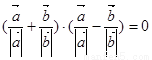 .其中正确的命题为___________.(写出所有正确命题的序号)
.其中正确的命题为___________.(写出所有正确命题的序号)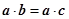 ,则
,则 ; ②已知
; ②已知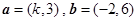 .若
.若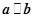 ,则
,则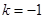 ;
;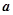 和
和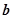 ,满足
,满足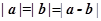 ,则
,则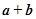 的夹角为
的夹角为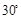 ;
;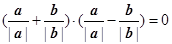 .
.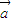 •
•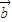 =
=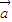 •
•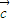 ,则
,则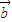 =
=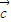 ,;
,;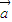 =(k,3),
=(k,3),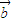 =(-2,6).若
=(-2,6).若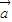 ∥
∥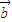 ,则k=-1.
,则k=-1.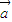 和
和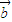 ,满足|
,满足|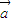 |=|
|=|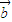 |=|
|=|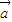 -
-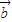 |,则
|,则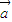 与
与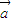 +
+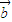 的夹角为30°.
的夹角为30°.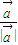 +
+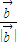 )•(
)•(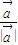 -
-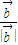 )=0.
)=0.