题目内容
将y=cosx的图象向左平移a个单位长度或向右平移b个单位长度(a、b均为正数),可得到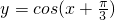 的图象,则|a-b|的最小值为
的图象,则|a-b|的最小值为
- A.

- B.

- C.

- D.2π
B
分析:将y=cosx的图象向左平移a个单位长度或向右平移b个单位长度(a、b均为正数),可得到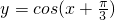 的图象进而求得a,再由诱导公式可得b的值.即可求得|a-b|的最小值.
的图象进而求得a,再由诱导公式可得b的值.即可求得|a-b|的最小值.
解答:将y=cosx的图象向左平移a个单位长度(a为正数),可得到y=cos(x+a)
即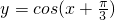 =cos(x+a)的图象,∴
=cos(x+a)的图象,∴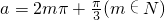 ;
;
将y=cosx的图象向右平移b个单位长度(b为正数),可得到y=cos(x+b)
即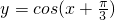 =cos(x-b)的图象,∴
=cos(x-b)的图象,∴ .
.
则|a-b|=|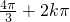 |(k∈Z),所以|a-b|的最小值是
|(k∈Z),所以|a-b|的最小值是 .
.
故答案选B.
点评:本题主要考查三角函数的平移与恒等变换.三角函数的平移原则为左加右减上加下减.
分析:将y=cosx的图象向左平移a个单位长度或向右平移b个单位长度(a、b均为正数),可得到
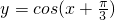 的图象进而求得a,再由诱导公式可得b的值.即可求得|a-b|的最小值.
的图象进而求得a,再由诱导公式可得b的值.即可求得|a-b|的最小值.解答:将y=cosx的图象向左平移a个单位长度(a为正数),可得到y=cos(x+a)
即
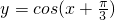 =cos(x+a)的图象,∴
=cos(x+a)的图象,∴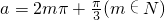 ;
;将y=cosx的图象向右平移b个单位长度(b为正数),可得到y=cos(x+b)
即
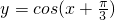 =cos(x-b)的图象,∴
=cos(x-b)的图象,∴ .
.则|a-b|=|
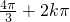 |(k∈Z),所以|a-b|的最小值是
|(k∈Z),所以|a-b|的最小值是 .
.故答案选B.
点评:本题主要考查三角函数的平移与恒等变换.三角函数的平移原则为左加右减上加下减.

练习册系列答案
相关题目