题目内容
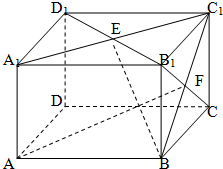 如图,在长方体AC1中,AB=BC=2,AA1=
如图,在长方体AC1中,AB=BC=2,AA1=| 2 |
(1)求异面直线AF和BE所成的角;
(2)求直线AF和平面BEC所成角的余弦值.
分析:(1)根据所给的长方体,以D为坐标原点DA、DC、DD1为x,y,z轴建立空间直角坐标系,写出点的坐标,得出对应的向量的坐标,根据两个向量的数量积为0,得到夹角.
(2)根据上一问做出的坐标系和点的坐标,写出要用的点的坐标,设出平面的法向量,根据法向量与平面上的向量数量积等于0,得到一个法向量.
(2)根据上一问做出的坐标系和点的坐标,写出要用的点的坐标,设出平面的法向量,根据法向量与平面上的向量数量积等于0,得到一个法向量.
解答: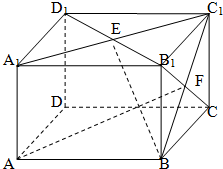 解:(1)如图,以D为坐标原点DA、DC、DD1为x,y,z轴建立空间直角坐标系,
解:(1)如图,以D为坐标原点DA、DC、DD1为x,y,z轴建立空间直角坐标系,
则:A(2,0,0),F(1,2,
)
B(2,2,0),E(1,1,
),C(0,2,0)
∴
=(-1,2,
),
=(-1,-1,
),
∴
•
=1-2+1=0
所以AF和BE所成的角为90°,
(2)设平面BEC的一个法向量为
=(x,y,z),又
=(-2,0,0),
=(-1,-1,
),
则:
•
=-2x=0
•
=-x-y+
z=0
∴x=0,令z=1,则:y=
∴
=(0,
,1)
∴cos<
,
>=
=
=
设直线AF和平面BEC所成角为θ则:Sinθ=
∴cosθ=
即直线AF和平面BEC所成角的余弦值为
 解:(1)如图,以D为坐标原点DA、DC、DD1为x,y,z轴建立空间直角坐标系,
解:(1)如图,以D为坐标原点DA、DC、DD1为x,y,z轴建立空间直角坐标系,则:A(2,0,0),F(1,2,
| ||
| 2 |
B(2,2,0),E(1,1,
| 2 |
∴
| AF |
| ||
| 2 |
| BE |
| 2 |
∴
| AF |
| BE |
所以AF和BE所成的角为90°,
(2)设平面BEC的一个法向量为
| n |
| BC |
| BE |
| 2 |
则:
| n |
| BC |
| n |
| BE |
| 2 |
∴x=0,令z=1,则:y=
| 2 |
| n |
| 2 |
∴cos<
| AF |
| n |
| ||||
|
|
| ||||||
|
5
| ||
| 33 |
设直线AF和平面BEC所成角为θ则:Sinθ=
5
| ||
| 33 |
∴cosθ=
2
| ||
| 33 |
即直线AF和平面BEC所成角的余弦值为
2
| ||
| 33 |
点评:本题考查两条异面直线所成的角和线面角,本题解题的关键是建立坐标系,把理论的推导变成了数字的运算,从而降低了题目的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在长方体AC1中,AB=BC=2,
如图,在长方体AC1中,AB=BC=2,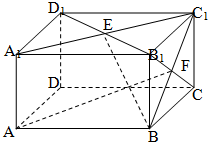 如图,在长方体AC1中,
如图,在长方体AC1中,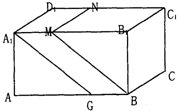 如图,在长方体AC1中,分别过BC和A1D1的两个平行平面如果将长方体分成体积相等的三个部分,那么
如图,在长方体AC1中,分别过BC和A1D1的两个平行平面如果将长方体分成体积相等的三个部分,那么 ,E.F分别是面A1C1.面BC1的中心,求(1)AF和BE所成的角.
,E.F分别是面A1C1.面BC1的中心,求(1)AF和BE所成的角.