题目内容
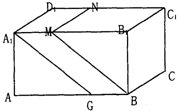 如图,在长方体AC1中,分别过BC和A1D1的两个平行平面如果将长方体分成体积相等的三个部分,那么
如图,在长方体AC1中,分别过BC和A1D1的两个平行平面如果将长方体分成体积相等的三个部分,那么| C1N | ND1 |
2
2
.分析:由已知中长方体AC1中,分别过BC和A1D1的两个平行平面如果将长方体分成体积相等的三个部分,由于所分的三部分为等高的棱柱,故三个柱体的底面面积相等;进而根据三角形MBB1与四边形A1GBM是等高的图形,得到其底边之比.
解答:解:∵长方体AC1中,分别过BC和A1D1的两个平行平面如果将长方体分成体积相等的三个部分
故S△A1AG=SA1GBM=S△MBB1
∴
=
=
=2
故答案为:2
故S△A1AG=SA1GBM=S△MBB1
∴
| C1N |
| ND1 |
| A1M |
| MB1 |
| 2 |
| 1 |
故答案为:2
点评:本题考查的知识点是棱柱的体积公式,其中利用转化思想,根据长方体AC1中,分别过BC和A1D1的两个平行平面所分的三部分为同高柱体,转化为面积相等,再根据平面图形也为同高图形,进而转化为底面边长之比,是解答此类问题的关键.

练习册系列答案
相关题目
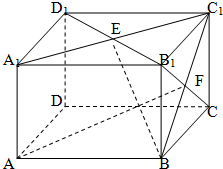 如图,在长方体AC1中,
如图,在长方体AC1中, 如图,在长方体AC1中,AB=BC=2,
如图,在长方体AC1中,AB=BC=2,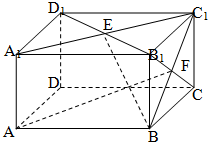 如图,在长方体AC1中,
如图,在长方体AC1中, ,E.F分别是面A1C1.面BC1的中心,求(1)AF和BE所成的角.
,E.F分别是面A1C1.面BC1的中心,求(1)AF和BE所成的角.