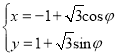题目内容
【题目】如图，过抛物线
焦点
的直线交抛物线于
，
两点，记以，为直径端点的圆为圆
.
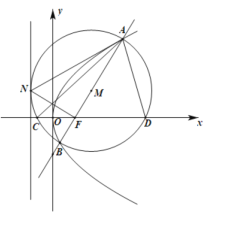
（1）证明：圆与抛物线的准线相切；
（2）设
，点在焦点的右侧，圆与
轴交于
，
两点，记
和
的面积为
，
求
的最大值（其中，点
为圆与抛物线准线的切点）
【答案】（1）证明见解析；（2）
.
【解析】
（1）设直线
，与抛物线方程联立，利用焦点弦公式求出
，结合韦达定理求出
的坐标，求得到准线的距离
，命题得证；
（2）由题意得出抛物线方程，联立直线和抛物线的方程，结合韦达定理及弦长公式，写出
，
的表达式，结合基本不等式得到结果.
（1）设直线，
联立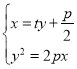
，得
﹐
设
，
则
，
∴
，
，
∴
∵抛物线的准线方程为
∴点到准线的距离
∴圆与抛物线的准线相切.
（2）设
，与
联立，得
，
则
，
∴
，
，
∴
∵抛物线的准线方程为
，且点
为圆与抛物线准线的切点
∴
，
∵圆与
轴交于
，
两点
∴
，
∵
﹐
﹐
∴
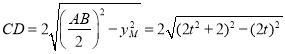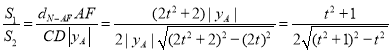
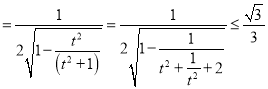
当
时，等号成立，
最大值为
【题目】（本小题满分12分）某商场为了了解顾客的购物信息，随机的在商场收集了100位顾客购物的相关数据，整理如下：
一次购物款（单位：元） | [0,50） | [50,100） | [100,150） | [150,200） | [200,+∞） |
顾客人数 | m | 20 | 30 | n | 10 |
统计结果显示100位顾客中购物款不低于100元的顾客占60%，据统计该商场每日大约有5000名顾客，为了增加商场销售额度，对一次性购物不低于100元的顾客发放纪念品（每人一件）．（注：视频率为概率）
（1）试确定
的值，并估计该商场每日应准备纪念品的数量；
（2）为了迎接店庆，商场进行让利活动，一次购物款200元及以上的一次返利30元；一次性购物
款小于200元的按购物款的百分比返利，具体见下表：
一次购物款（单位：元） | [0,50） | [50,100） | [100,150） | [150,200） |
返利百分比 | 0 | 6% | 8% | 10% |
估计该商场日均让利多少元？