题目内容
有以下四个命题:①f(x)=
| 1 |
| x |
②若f(x)是(a,b)内的连续函数,则f(x)在(a,b)内有最大值和最小值;
③
| lim | ||
x→
|
| 2sin2x |
| cosx |
④若f(x)=
|
| lim |
| x→0 |
其中正确命题的序号是
分析:①f(x)=
在x=0处无意义,故不正确;②举例说明即可,与若f(x)是[a,b]内的连续函数,则f(x)在[a,b]内有最大值和最小值矛盾;③属于
型的求极限,根据罗比特法则即可求得结果;④f(x)=
求出其左右极限,看是否相等,如果相等且为0,就正确,否则不正确.
| 1 |
| x |
| 0 |
| 0 |
|
解答:解:①f(x)=
的定义域是{x|x≠0},故①不正确;
②如函数f(x)=x在区间(1,2)上连续,但是既没有最大值也没有最小值;故②不正确;
③
=
=4
=4,故③正确;
④
f(x)=0,
f(x)=0+1=1
∴
f(x)不存在.
故答案为③.
| 1 |
| x |
②如函数f(x)=x在区间(1,2)上连续,但是既没有最大值也没有最小值;故②不正确;
③
| lim | ||
x→
|
| 2sin2x |
| cosx |
| lim | ||
x→
|
| 4cos2x |
| -sinx |
cos2×
| ||
-sin
|
④
| lim |
| x→x0+ |
| lim |
| x→x0- |
∴
| lim |
| x→0 |
故答案为③.
点评:此题是个容易题.考查函数的连续性和极限及其运算,判断命题真假,如果说明它是正确的,必须给以证明,反之,举出反例即可.考查学生分析问题、解题问题的能力.

练习册系列答案
相关题目
 ),有以下四个命题:①f(x)为奇函数;②f(x)的最小正周期为π,③f(x)在(0,
),有以下四个命题:①f(x)为奇函数;②f(x)的最小正周期为π,③f(x)在(0, )上单调递减,④x=
)上单调递减,④x= 是f(x)的一条对称轴.其中真命题有( )
是f(x)的一条对称轴.其中真命题有( ) ),有以下四个命题:①f(x)为奇函数;②f(x)的最小正周期为π,③f(x)在(0,
),有以下四个命题:①f(x)为奇函数;②f(x)的最小正周期为π,③f(x)在(0,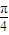 )上单调递减,④x=
)上单调递减,④x=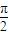 是f(x)的一条对称轴.其中真命题有( )
是f(x)的一条对称轴.其中真命题有( ) ,有以下四个命题:
,有以下四个命题: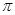 ;③f(x)在(
;③f(x)在( )上单调递减;④
)上单调递减;④ 是f(x)的一条对称轴,其中真命题有 (把所有正确命题的序号都填上)
是f(x)的一条对称轴,其中真命题有 (把所有正确命题的序号都填上)