题目内容

【题目】从正方体的八个顶点中任取三个点作三角形，直角三角形的个数为__________．

【答案】48

【解析】

由题意可得有两种情况:所选的三个顶点在同一个表面和不在同一个表面,若取的三个顶点在同一个表面,则由组合知识点可求得直角三角形的个数;若取的三个顶点不在同一个表面,则可考虑一条棱可组成直角三角形的个数,然后乘以棱数即可求出这种情况下直角三角形的个数,最后综合两种情况即可得出最终答案.

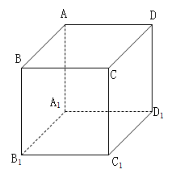
如图所示:当选取的三个顶点在正方体同一表面时,那么同一表面的四个顶点可组成的三角形的个数为,则可组成的直角三角形的个数为:64=24;

当选取的三个顶点不在正方体同一个表面时,选AB棱可组成的直角三角形的为:△ABC1和△ABD1共计2个,所以三个顶点不在同一表面时可组成的直角三角形的个数为212=24;

综上可得正方体八个点任取三个可组成直角三角形的个数为24+24=48个.

故答案为:48.

练习册系列答案
相关题目

【题目】朱世杰是历史上最伟大的数学家之一，他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题：今有官司差夫一千八百六十四人筑堤，只云初日差六十四人，次日转多七人.”其大意为“官府陆续派遣1864人前往修筑堤坝，第一天派出64人，从第二天开始每天派出的人数比前一天多7人.”在该问题中的1864人全部派遣到位需要的天数为（ ）

A. 9B. 16C. 18D. 20

【题目】某中学2018年的高考考生人数是2015年高考考生人数的倍，为了更好地对比该校考生的升学情况，统计了该校2015年和2018年的高考情况，得到如图柱状图：

则下列结论正确的是　　

A. 与2015年相比，2018年一本达线人数减少

B. 与2015年相比，2018年二本达线人数增加了倍

C. 2015年与2018年艺体达线人数相同

D. 与2015年相比，2018年不上线的人数有所增加

【题目】如图，已知城市周边有两个小镇、，其中乡镇位于城市的正东方处，乡镇与城市相距，与夹角的正切值为2，为方便交通，现准备建设一条经过城市的公路，使乡镇和分别位于的两侧，过和建设两条垂直的公路和，分别与公路交汇于、两点，以为原点，所在直线为轴，建立如图所示的平面直角坐标系.

（1）当两个交汇点、重合，试确定此时路段长度；

（2）当，计算此时两个交汇点、到城市的距离之比；

（3）若要求两个交汇点、的距离不超过，求正切值的取值范围.

【题目】设直线l的方程为y=(-a-1)x +a-2.

（1）求直线过定点A的坐标；

（2）若l在两坐标轴上的截距相等，求l的方程；

（3）若l不经过第二象限，求实数a的取值范围.

【题目】直线与双曲线相交于、两点，为坐标原点，且．

（1）求与满足的关系；

（2）求证：点到直线的距离是定值，并求的最小值．

【题目】如图，在多面体中，是等边三角形，是等腰直角三角形， ，平面平面，平面.

(1) 求证：；

(2) 若，求直线与平面所成角的正弦值.

【题目】若三次函数（）的图象上存在相互平行且距离为的两条切线，则称这两条切线为一组“距离为的友好切线组”.已知，则函数的图象上“距离为4的友好切线组”有（ ）组？

A. 0B. 1C. 2D. 3

【题目】四棱锥的底面为直角梯形，，，，为正三角形.

（1）点为棱上一点，若平面，，求实数的值；

（2）求点B到平面SAD的距离.

【答案】（1）；（2）

【解析】试题分析：（1）由平面，可证，进而证得四边形为平行四边形，根据，可得；

（2）利用等体积法可求点到平面的距离.

试题解析：（（1）因为平面SDM，

平面ABCD，

平面SDM 平面ABCD=DM，

所以，

因为，所以四边形BCDM为平行四边形，又，所以M为AB的中点.

因为，

.

（2）因为 ， ，

所以平面，

又因为平面，

所以平面平面，

平面平面，

在平面内过点作直线于点，则平面，

在和中，

因为，所以，

又由题知，

所以，

由已知求得，所以，

连接BD，则，

又求得的面积为，

所以由点B 到平面的距离为.

【题型】解答题
【结束】
19

【题目】小明在石家庄市某物流派送公司找到了一份派送员的工作，该公司给出了两种日薪薪酬方案.甲方案：底薪100元，每派送一单奖励1元；乙方案：底薪140元，每日前55单没有奖励，超过55单的部分每单奖励12元.

（1）请分别求出甲、乙两种薪酬方案中日薪（单位：元）与送货单数的函数关系式；

（2）根据该公司所有派送员100天的派送记录，发现派送员的日平均派送单数满足以下条件：在这100天中的派送量指标满足如图所示的直方图，其中当某天的派送量指标在 时，日平均派送量为单.

若将频率视为概率，回答下列问题：

①根据以上数据，设每名派送员的日薪为（单位：元），试分别求出甲、乙两种方案的日薪的分布列，数学期望及方差；

②结合①中的数据，根据统计学的思想，帮助小明分析，他选择哪种薪酬方案比较合适，并说明你的理由.

（参考数据： ， ， ， ， ， ， ， ， ）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网