Question

（2010•安徽模拟）设M是正△P₁P₂P₃及其内部的点所构成的集合，点P₀是正△P₁P₂P₃的中心，若集合S={P|P∈M，|PP₀|≤|PP_i|，i=1，2，3}，在M中任取一点落在S中的概率为（　　）

• A．

  1

  3

• B．

  1

  4

• C．

  2

  3

• D．

  1

  2

Answer 1

分析：关键是集合S在哪里，由于满足|PP₀|=|PP_i|，i=1，2，3的点P在线段P₀P_i（i=1，2，3）的中垂线上，由此即可知集合S形状，求其面积，而集合M的图象为正三角形，求其面积，最后事件发生的概率为小面积比大面积

解答：解：如图，M点的活动空间为正△P₁P₂P₃及其内部，其面积为

3

4

a2，（a为三角形边长）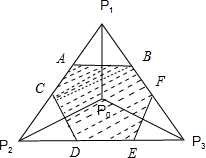
设事件A={M点落在S中}，满足事件A的点M的活动空间为如图阴影部分，（其中线段AB，CD，EF，分别为线段P₀P_i（i=1，2，3）的中垂线）
其面积为

3

4

a2-3×

3

4

(

a

3

)2=

3

6

a2
∴P（A）=

3 6 a2

3 4 a2

=

2

3

故选C

点评：本题考查了几何概型的意义和求法，找到事件发生时的图形并求其面积是解决问题的关键