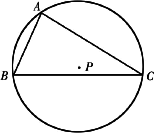Question

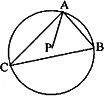
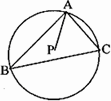
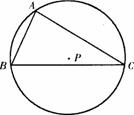
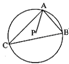如图，点P为△ABC的外心，且|

AC

|=4，|

AB

|=2，则

AP

•(

AC

-

AB

)等于（　　）

A．2

B．4

C．6

D．8

Answer 1

分析：根据向量数量积的公式，结合三角形外心的性质可得可得

AP

•

AC

=

|AP

|•|

AC

|cos∠PAD=

1

2

|

AC

|2=8，同理可得

AP

•

AB

=

1

2

|

AB

|2=2，利用向量数量积运算法则计算即可．

解答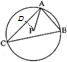：解：作PD⊥AC于D，则
∵P为△ABC的外心，∴

AD

=

1

2

AC

，
可得

AP

•

AC

=

|AP

|•|

AC

|cos∠PAD=

1

2

|

AC

|2=8
同理可得

AP

•

AB

=

1

2

|

AB

|2=2

AP

•(

AC

-

AB

)=

AP

•

AC

-

AP

•

AB

=6
故选C

点评：本题在三角形中给出外心，求向量数量积的式子．着重考查了三角形的外心的性质、向量数量积的定义与运算性质等知识，属于中档题．