题目内容
已知向量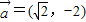
，
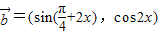（x∈R）．设函数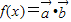
（1）求
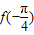的值； （2）求函数f（x）在区间
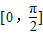上的值域．
【答案】分析：（1）利用向量的坐标运算可求得f（x）=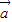
•
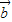，从而可求得f（-
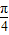）的值；
（2）由（1）知f（x）=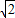
sin（2x-
），由x∈[0，
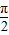]⇒2x-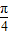
∈[-
，
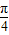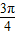]，利用正弦函数的单调性质即可求f（x）在x∈[0，
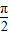]上的值域．
解答：解：（1）∵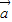
=（
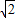，-2），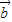
=（sin（
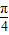+2x），cos2x），
∴f（x）=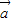
•
=
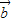
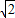sin（
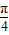+2x）-2cos2x
=
（
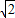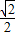cos2x+
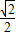sin2x）-2cos2x
=sin2x-cos2x
=
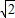sin（2x-
），
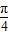∴f（-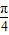
）=
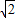sin（-
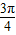）=-1；
（2）∵x∈[0，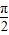
]，
∴2x-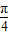
∈[-
，
]，
∴-
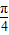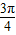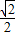≤sin（2x-
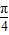）≤1，-1≤
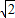sin（2x-
）≤
．
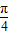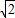∴f（x）在x∈[0，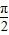
]上的值域为[-1，
]．
点评：本题考查平面向量数量积的坐标表示，考查三角函数中的恒等变换应用，考查复合三角函数的单调性，属于中档题．
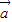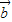•，从而可求得f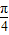（-）的值；（2）由（1）知f（x）=
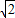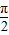sin（2x-），由x∈[0，]⇒2x-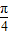∈[-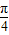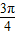，]，利用正弦函数的单调性质即可求f（x）在x∈[0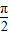，]上的值域．解答：解：（1）∵
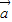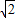=（，-2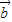），=（sin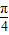（+2x），cos2x），∴f（x）=
•=
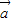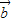
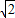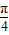sin（+2x）-2cos2x=
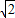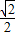（cos2x+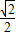sin2x）-2cos2x=sin2x-cos2x
=
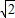sin（2x-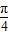），∴f（-
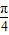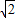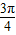）=sin（-）=-1；（2）∵x∈[0，
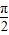]，∴2x-
∈[-，]，∴-
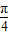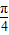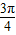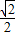≤sin（2x-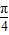）≤1，-1≤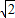sin（2x-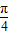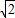）≤．∴f（x）在x∈[0，
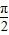]上的值域为[-1，]．点评：本题考查平面向量数量积的坐标表示，考查三角函数中的恒等变换应用，考查复合三角函数的单调性，属于中档题．
练习册系列答案
互动英语系列答案
相关题目
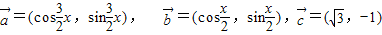，其中x∈R，
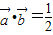时，求x值的集合；
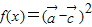，求f（x）的最小正周期及其单调增区间．
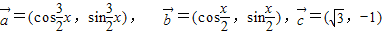，其中x∈R，
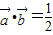时，求x值的集合；
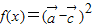，求f（x）的最小正周期及其单调增区间．
，
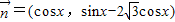，x∈R，设
．
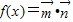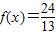，且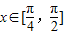
，求sin2x的值．
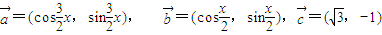，其中x∈R，
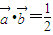时，求x值的集合；
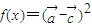，求f（x）的最小正周期及其单调增区间．
，
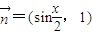（x∈R），设函数
．
，
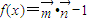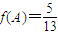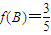，求f（C）的值．