题目内容
已知向量
，
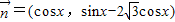，x∈R，设
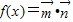．（1）求函数f（x）的最小正周期．
（2）若
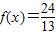，且
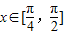，求sin2x的值．
【答案】分析：（1）根据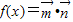
，结合向量
，
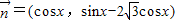，我们易得函数f（x）的解析式，利用辅助角公式将其化为正弦型函数的形式，再利用T=
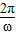，即可求出函数的最小正周期．
（2）由（1）中函数解析式，根据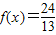
，我们可求出sin（2x+
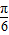）的值，结合
，我们还可以求出cos（2x+
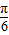）的值，根据sin2x=sin[（2x+
）-
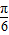]代入两名差的正弦公式，即可求出答案．
解答：解：（1）∵
=cos2x-sin2x+2
sinxcosx=cos2x+
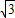sin2x=2sin（2x+
）
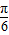∴函数f（x）的最小正周期T=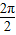
=π
（2）∵f（x）=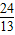
，
∴sin（2x+
）=
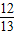
又∵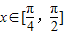
，
∴cos（2x+
）=-
=-
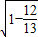即sin2x=sin[（2x+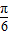
）-
]
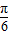=sin（2x+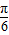
）cos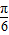
-cos（2x+
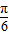）sin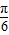
=
×
-（-
）×
=
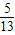点评：本题考查的知识点是平面向量的数量积运算，二倍角公式，辅助角公式，最小正周期的求法，给值求值及两角差的正弦公式，处理的关键（1）中要将函数的解析式化为正弦型函数；（2）中要分析已知角与未知角之间的关系，以选取恰当的公式．
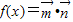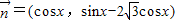，结合向量，，我们易得函数f（x）的解析式，利用辅助角公式将其化为正弦型函数的形式，再利用T=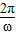，即可求出函数的最小正周期．（2）由（1）中函数解析式，根据
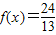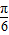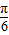，我们可求出sin（2x+）的值，结合，我们还可以求出cos（2x+）的值，根据sin2x=sin[（2x+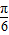）-]代入两名差的正弦公式，即可求出答案．解答：解：（1）∵
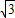=cos2x-sin2x+2sinxcosx=cos2x+sin2x=2sin（2x+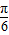）∴函数f（x）的最小正周期T=
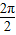=π（2）∵f（x）=
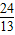，∴sin（2x+
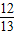
）=又∵
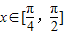，∴cos（2x+
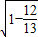）=-=-即sin2x=sin[（2x+
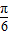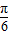）-]=sin（2x+
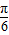）cos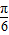-cos（2x+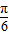）sin=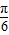
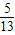×-（-）×=点评：本题考查的知识点是平面向量的数量积运算，二倍角公式，辅助角公式，最小正周期的求法，给值求值及两角差的正弦公式，处理的关键（1）中要将函数的解析式化为正弦型函数；（2）中要分析已知角与未知角之间的关系，以选取恰当的公式．
练习册系列答案
口算能手系列答案
相关题目
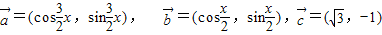，其中x∈R，
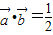时，求x值的集合；
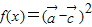，求f（x）的最小正周期及其单调增区间．
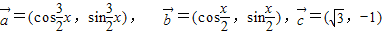，其中x∈R，
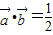时，求x值的集合；
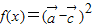，求f（x）的最小正周期及其单调增区间．
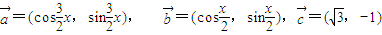，其中x∈R，
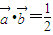时，求x值的集合；
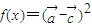，求f（x）的最小正周期及其单调增区间．
，
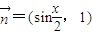（x∈R），设函数
．
，
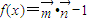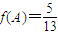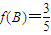，求f（C）的值．