题目内容
(1)将下列曲线的直角坐标方程化为极坐标方程:①(x2+y2)2=
(2)将下列曲线的极坐标方程化为直角坐标方程:
①ρ2=cos2θ;②ρ=![]() .
.
解:(1)①由(x2+y2)2=
∴ρ2=
②由x-3y=0,得ρcosθ-3ρsinθ=0,tanθ=![]() .
.
∴θ=arctan![]() .
.
(2)①ρ2=cos2θ两边同时乘以ρ2,得ρ4=ρ2cos2θ=(ρcosθ)2.
∴(x2+y2)2=x2,即有x2+y2=x或x2+y2=-x,它表示两个圆.
②方程可化为2ρ-ρcosθ=4,即2ρ=4+x,两边平方得4ρ2=(x+4)2.
4x2+4y2=x2+8x+16,
即3x2-8x+4y2=16.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求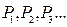 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对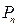 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求