题目内容
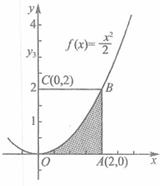 如图,利用随机模拟的方法可以估计图中由曲线y=
如图,利用随机模拟的方法可以估计图中由曲线y=| x2 |
| 2 |
①先产生两组0~1的均匀随机数,a=rand ( ),b=rand ( );
②做变换,令x=2a,y=2b;(3)产生N个点(x,y),并统计满足条件y<
| x2 |
| 2 |
分析:先由计算器做模拟试验结果试验估计,满足条件y<
的点(x,y)的概率,再转化为几何概型的面积类型求解.
| x2 |
| 2 |
解答:解:根据题意:满足条件y<
的点(x,y)的概率是
矩形的面积为10,设阴影部分的面积为s
则有
=
∴s=1.328
故答案为:1.328
| x2 |
| 2 |
| 332 |
| 1000 |
矩形的面积为10,设阴影部分的面积为s
则有
| S |
| 4 |
| 332 |
| 1000 |
∴s=1.328
故答案为:1.328
点评:本题主要考查模拟方法估计概率以及几何概型中面积类型,将两者建立关系,引入方程思想.

练习册系列答案
相关题目
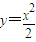 与两直线x=2及y=0所围成的阴影部分的面积S:
与两直线x=2及y=0所围成的阴影部分的面积S: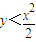 的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果,当N=1000时,N1=332,则据此可估计S的值为 .
的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果,当N=1000时,N1=332,则据此可估计S的值为 .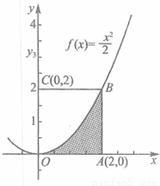
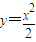 与两直线x=2及y=0所围成的阴影部分的面积S:
与两直线x=2及y=0所围成的阴影部分的面积S: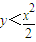 的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果,当N=1000时,N1=332,则据此可估计S的值为 .
的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果,当N=1000时,N1=332,则据此可估计S的值为 .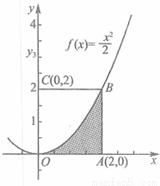
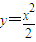 与两直线x=2及y=0所围成的阴影部分的面积S:
与两直线x=2及y=0所围成的阴影部分的面积S: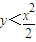 的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果,当N=1000时,N1=332,则据此可估计S的值为 .
的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果,当N=1000时,N1=332,则据此可估计S的值为 .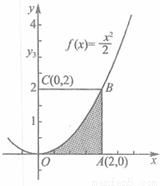
 与两直线x=2及y=0所围成的阴影部分的面积S:
与两直线x=2及y=0所围成的阴影部分的面积S: 的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果,当N=1000时,N1=332,则据此可估计S的值为 .
的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果,当N=1000时,N1=332,则据此可估计S的值为 .