题目内容
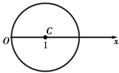 如图,在极坐标系中,圆C的圆心坐标为(1,0),半径为1.
如图,在极坐标系中,圆C的圆心坐标为(1,0),半径为1.(Ⅰ)求圆C的极坐标方程;
(Ⅱ)若以极点O为原点,极轴所在直线为x轴建立平面直角坐标系.已知直线l的参数方程为
|
分析:(Ⅰ)如图,设圆C上任意一点的极坐标D(ρ,θ),连接OD,BD.在Rt△OMD中,利用OM=OBcos∠MOD即可得出.
(II)消去参数t即可得到直线l的方程,把圆的极坐标方程化为直角坐标方程,利用点到直线的距离公式可得圆心到直线l的距离,与半径相比较即可判断出位置关系.
(II)消去参数t即可得到直线l的方程,把圆的极坐标方程化为直角坐标方程,利用点到直线的距离公式可得圆心到直线l的距离,与半径相比较即可判断出位置关系.
解答: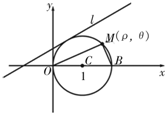 解:(Ⅰ)如图,设圆C上任意一点的极坐标D(ρ,θ),连接OD,BD.
解:(Ⅰ)如图,设圆C上任意一点的极坐标D(ρ,θ),连接OD,BD.
在Rt△OMD中,∵OM=OBcos∠MOD,∴ρ=2cosθ.
(Ⅱ)由直线l的参数方程为
(t为参数),消去参数t可得
l的普通方程为y=
(x+1),即直线l:x-
y+1=0,
由ρ=2cosθ,得圆C的直角坐标方程为(x-1)2+y2=1,
∵圆心到直线l的距离为d=
=1,
∴直线l与圆C的相切.
 解:(Ⅰ)如图,设圆C上任意一点的极坐标D(ρ,θ),连接OD,BD.
解:(Ⅰ)如图,设圆C上任意一点的极坐标D(ρ,θ),连接OD,BD.在Rt△OMD中,∵OM=OBcos∠MOD,∴ρ=2cosθ.
(Ⅱ)由直线l的参数方程为
|
l的普通方程为y=
| ||
| 3 |
| 3 |
由ρ=2cosθ,得圆C的直角坐标方程为(x-1)2+y2=1,
∵圆心到直线l的距离为d=
|1×1-
| ||
| 2 |
∴直线l与圆C的相切.
点评:熟练掌握把参数方程和极坐标方程化为普通方程、直线与圆的位置关系的判定方法是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
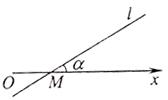
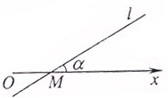 (2012•上海)如图,在极坐标系中,过点M(2,0)的直线l与极轴的夹角a=
(2012•上海)如图,在极坐标系中,过点M(2,0)的直线l与极轴的夹角a=
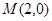 的直线
的直线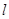 与极轴的夹角
与极轴的夹角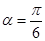 ,若将
,若将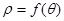 的形式,则
的形式,则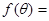
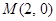 的直线
的直线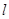 与极轴的夹角
与极轴的夹角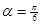 .若将
.若将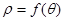 的形式,则
的形式,则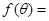 .
.