题目内容
已知点 在抛物线
在抛物线 上,那么
上,那么 到点
到点 的距离与点
的距离与点 到抛物线焦点距离之和取得最小值时,点
到抛物线焦点距离之和取得最小值时,点 的坐标为( ).
的坐标为( ).
A. | B. | C. | D. |
D
解析试题分析:点P到抛物线焦点距离等于点P到抛物线准线距离,如图PF+PQ=PS+PQ,故最小值在S,P,Q三点共线时取得,此时P,Q的纵坐标都是-1,故选D。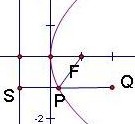
考点:本题主要考查抛物线的定义。
点评:典型题,抛物线是到定点与到定直线距离相等的点的集合。

练习册系列答案
相关题目
以抛物线 的焦点为圆心,且过坐标原点的圆的方程为( )
的焦点为圆心,且过坐标原点的圆的方程为( )
A. | B. |
C. | D. |
方程 表示焦点在
表示焦点在 轴的双曲线,则
轴的双曲线,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设抛物线顶点在坐标原点,,准线方程为 ,则抛物线方程是( )
,则抛物线方程是( )
A. | B. | C. | D. |
椭圆 上有n个不同的点:P1,P2, ,Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1,P2, ,Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于 的等差数列,则n的最大值是 ( )
的等差数列,则n的最大值是 ( )
| A.198 | B.199 |
| C.200 | D.201 |
已知△ABC的周长为20,且顶点B(0,-4),C(0,4),则顶点A的轨迹方程是
A. (x≠0) (x≠0) | B. (x≠0) (x≠0) |
C. (x≠0) (x≠0) | D. (x≠0) (x≠0) |




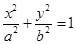 (a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )
(a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )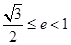
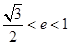
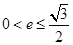
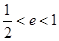
 ,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )



