题目内容
设sina-sinb=
,cosa+cosb=
,则cos(a+b)=______.
| 1 |
| 3 |
| 1 |
| 2 |
把sina-sinb=
和cosa+cosb=
两边分别平方得:
sin2a+sin2b-2sinasinb=
①,cos2a+cos2b+2cosacosb=
②,
①+②得:1+1+2cosacosb-2sinasinb=
,
则cos(a+b)=cosacosb-sinasinb=
×
=-
.
故答案为:-
.
| 1 |
| 3 |
| 1 |
| 2 |
sin2a+sin2b-2sinasinb=
| 1 |
| 9 |
| 1 |
| 4 |
①+②得:1+1+2cosacosb-2sinasinb=
| 13 |
| 36 |
则cos(a+b)=cosacosb-sinasinb=
| 13-72 |
| 36 |
| 1 |
| 2 |
| 59 |
| 72 |
故答案为:-
| 59 |
| 72 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
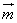 =(a,cosB),
=(a,cosB), =(b,cosA), 且
=(b,cosA), 且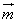 //
//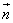 且
且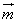 ≠
≠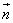 。
。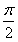 ,并求出sinA+sinB的取值范围;
,并求出sinA+sinB的取值范围; 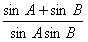 表示成t的函数f(t),并求出y=f(t)的值域。
表示成t的函数f(t),并求出y=f(t)的值域。  ,cosa+cosb=
,cosa+cosb= ,则cos(a+b)= .
,则cos(a+b)= . ,cosa+cosb=
,cosa+cosb= ,则cos(a+b)= .
,则cos(a+b)= .