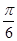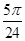题目内容
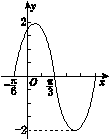
已知函数y=Asin(ωx+φ)+m(A>0,|φ|< )的最大值为4,最小值为0,两个对称轴间的最短距离为
)的最大值为4,最小值为0,两个对称轴间的最短距离为 ,直线x=
,直线x= 是其图象的一条对称轴,则符合条件的解析式是( ).
是其图象的一条对称轴,则符合条件的解析式是( ).
A.y=4sin | B.y=-2sin +2 +2 |
C.y=-2sin +2 +2 | D.y=2sin +2 +2 |
A
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知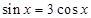 ,则
,则 的值是( )
的值是( )
A.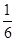 | B. | C. | D.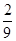 |
函数y=- cos2x+
cos2x+ 的递增区间是( )
的递增区间是( )
A.(kπ,kπ+ )(k∈Z) )(k∈Z) |
B.(kπ+ ,kπ+π)(k∈Z) ,kπ+π)(k∈Z) |
| C.(2kπ,2kπ+π)(k∈Z) |
| D.(2kπ+π,2kπ+2π)(k∈Z) |
将函数y=sin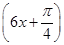 的图像上各点向右平移
的图像上各点向右平移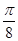 个单位,则得到新函数的解析式为( )
个单位,则得到新函数的解析式为( )
A.y=sin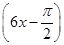 | B.y=sin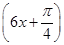 | C.y=sin | D.y=sin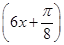 |
已知ω>0,函数f(x)=sin  在
在 上单调递减,则ω的取值范围是( ).
上单调递减,则ω的取值范围是( ).
A. | B. | C. | D.(0,2] |
已知f(x)=sin2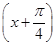 ,若a=f(lg 5),b=f
,若a=f(lg 5),b=f ( ).
( ).
| A.a+b=0 | B.a-b=0 | C.a+b=1 | D.a-b=1 |
函数y=sin x+cos x的最大值和最小正周期分别是( ).
A.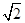 ,π ,π | B.2,π | C.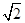 ,2π ,2π | D.2,2π |
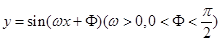 一个周期内的图象上的四个点,如图所示,
一个周期内的图象上的四个点,如图所示, B为
B为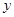 轴上的点,C为图像上的最低点,E为该函数图像的一个对称中心,B与D关于点E对称,
轴上的点,C为图像上的最低点,E为该函数图像的一个对称中心,B与D关于点E对称, 在
在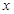 轴上的投影为
轴上的投影为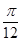 ,则
,则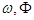 的值为( )
的值为( )
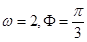 B.
B.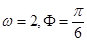
 D.
D.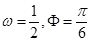
 的部分图像如图所示,当x∈0,
的部分图像如图所示,当x∈0,