题目内容
已知函数 的图像关于直线
的图像关于直线 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为 .
.
(1)求 和
和 的值;
的值;
(2)若 ,求
,求 的值.
的值.
(1)ω=2, ;(2)
;(2) .
.
解析试题分析:(1)由题意可得函数f(x)的最小正周期为π 求得ω=2.再根据图象关于直线 对称,结合
对称,结合 可得 φ 的值.(2)由条件求得
可得 φ 的值.(2)由条件求得 再根据
再根据 的范围求得
的范围求得 的值,再根据
的值,再根据 ,利用两角和的正弦公式计算求得结果.
,利用两角和的正弦公式计算求得结果.
试题解析:(1)因为f(x)图像上相邻两个最高点的距离为 ,所以f(x)的最小正周期
,所以f(x)的最小正周期 ,从而
,从而 ,又因f(x)的图象关于直线
,又因f(x)的图象关于直线 对称,所以
对称,所以 ,又因为
,又因为 得
得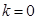 ,所以
,所以 .
.
(2)由(1)得 所以
所以 ,又
,又 得
得 所以
所以 ,因此
,因此
 .
.
考点:三角函数的周期公式,诱导公式,三角函数 的图像与性质,角的变换,两角和的正弦公式,同角三角函数的基本关系(平方关系).
的图像与性质,角的变换,两角和的正弦公式,同角三角函数的基本关系(平方关系).

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目


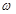 ;
; ,且
,且 ,求
,求 的值.
的值. 在区间
在区间 上的图像(完成列表并作图)。
上的图像(完成列表并作图)。



 ,再将图像沿
,再将图像沿 轴向右平移
轴向右平移 个单位,得到函数
个单位,得到函数 的图像.
的图像. .
. 上的值域.
上的值域. ,
, 图象的一条对称轴是直线
图象的一条对称轴是直线 .
. ;
; 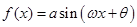 的部分图象如下图,其中
的部分图象如下图,其中
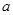 是
是 的角
的角 所对的边.
所对的边. 的解析式;
的解析式; 中角
中角 所对的边
所对的边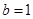 ,
, ,求
,求 .
.
 .
. 的最小正周期;
的最小正周期; 的图像向右、向上分别平移
的图像向右、向上分别平移 个单位长度得到
个单位长度得到 的图像,求
的图像,求 的最大值.
的最大值. 的终边上有一点
的终边上有一点 ,则
,则 的值是_____________.
的值是_____________.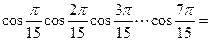 _________
_________