题目内容
(理)已知A、B、C是直线l上的三点,向量(1)求函数y=f(x)的表达式;
(2)若g(x)在点(3,g(3))处的切线与直线7x-18y+3=0平行,求函数g(x)的极值;
(3)若函数g(x)在(0,2)上单调递减,求实数a的取值范围.
(文)已知A、B、C是直线l上的三点,且满足:![]() -(y+ax2)
-(y+ax2)![]() +(x3+3x)
+(x3+3x)![]() =0.
=0.
(1)若f(x)在点(1,f(3))处的切线与直线2x+y+3=0平行,求函数y=f(x)的极值;
(2)若函数y=f(x)在(-2,![]() )上单调递减,求实数口的取值范围.
)上单调递减,求实数口的取值范围.
答案:(理)(1)∵![]() -[y+2f′(1)]
-[y+2f′(1)]![]() +ln(x+1)
+ln(x+1)![]() =0,
=0,
∴![]() =[y+2f′(1)]
=[y+2f′(1)]![]() -ln(x+1)
-ln(x+1)![]()
由于A、B、C三点共线,即[y+2f′(1)]+[-ln(x+1)]=1
∴y=f(x)=ln(x+1)+1-2f′(1)
f′(x)=![]() ,得f′(1)=
,得f′(1)=![]() ,故f(x)=ln(x+1).
,故f(x)=ln(x+1).
(2)∵g(x)=![]() +aln(x+1),
+aln(x+1),
∴g′(x)=![]() ,
,
又x∈(-1,0)∪(0,+∞)
由g′(3)=![]() ,解得a=2
,解得a=2
则g′(x)=![]()
由g′(x)>0解得-1<x<![]() 或x>1,由g′(x)<0
或x>1,由g′(x)<0
解得![]() <x<1
<x<1
则g(x)的增区间是(-1,![]() ),(1,+∞)
),(1,+∞)
g(x)的减区间是(![]() ,0),(0,1)
,0),(0,1)
故g极大值(x)=g(![]() )=-2-ln2,
)=-2-ln2,
g极小值(x)=g(1)=1+21n2.
(3)由g′(x)=![]() <0,得ax2-x-1<0,即a<
<0,得ax2-x-1<0,即a<![]() 在(0,2)上恒成立,
在(0,2)上恒成立,
令u=![]() ,
,
则u在t=![]() ∈(
∈(![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴u的最小值趋向于(![]() )2
)2![]() ,但取不到此值
,但取不到此值
∴a≤![]() .
.
(文)∵![]() -(y+ax2)
-(y+ax2)![]() +(x3+3x)
+(x3+3x)![]() =0,
=0,
∴![]() =(y+ax2)
=(y+ax2)![]() -(x3+3x)
-(x3+3x)![]()
由于A、B、C三点共线,得y+ax2-x3=1,即y=x3-ax2+3x+1.
(1)∵f′(x)=3x2-2ax+3,则f′(1)=3x2-2ax+3=3-2a+3=-2,得a=4,
∴f′(x)=3x2-8x+3=3(x-3)(x![]() ),
),
由f′(x)>0解得x<![]() 或x>3;
或x>3;
由f′(x)<0解得![]() <x<3.
<x<3.
则f(x)的增区间是(-∞,![]() ),(3,+∞);减区间是(
),(3,+∞);减区间是(![]() ,3)
,3)
故f极大值(x)=f(![]() )=
)=![]() ,f极小值(x)=f(3)=1.
,f极小值(x)=f(3)=1.
(2)∵f′(x)=3x2-2ax+3,
又f(x)在(-2,![]() )上单调递减,
)上单调递减,
∴f′(x)=3x2-2ax+3<0在(-2,![]() )上恒成立f′(x)max<0.
)上恒成立f′(x)max<0.
又∵f′(x)是开口向上的抛物线,
∴只要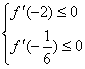 ,即
,即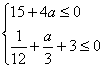 ,
,
解得a≤![]() .
.
