题目内容
在复数范围内，求方程|z|2+（z+
）i=1-i（i为虚数单位）的解．
解：原方程化简为|z|2+（z+）i=1-i，
设z=x+yi（x、y∈R），代入上述方程得x2+y2+2xi=1-i，
∴x2+y2=1且2x=-1，解得x=-
且y=±
，
∴原方程的解是z=-±i．
分析：设出复数z=x+yi（x、y∈R），代入|z|2+（z+）i=1-i，利用复数相等，求出x，y的值即可．
点评：本题考查复数的基本概念，复数相等，考查计算能力，是基础题．
）i=1-i，设z=x+yi（x、y∈R），代入上述方程得x2+y2+2xi=1-i，
∴x2+y2=1且2x=-1，解得x=-
且y=±，∴原方程的解是z=-
±i．分析：设出复数z=x+yi（x、y∈R），代入|z|2+（z+
）i=1-i，利用复数相等，求出x，y的值即可．点评：本题考查复数的基本概念，复数相等，考查计算能力，是基础题．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
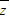）i=1-i（i为虚数单位）的解．