题目内容
在 中,角
中,角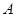 、
、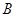 、
、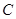 的对边分别为
的对边分别为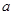 、
、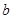 、
、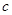 ,若
,若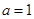 ,
,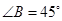 ,
, 的面积
的面积 ,则
,则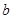 边长为 .
边长为 .
【答案】
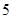 .
.
【解析】
试题分析: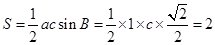 ,所以
,所以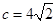 ,由余弦定理得
,由余弦定理得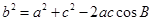
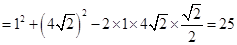 ,因此
,因此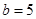 .
.
考点:1.三角形的面积公式;2.余弦定理

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
题目内容
在 中,角
中,角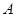 、
、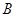 、
、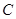 的对边分别为
的对边分别为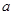 、
、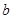 、
、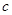 ,若
,若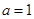 ,
,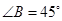 ,
, 的面积
的面积 ,则
,则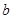 边长为 .
边长为 .
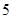 .
.
【解析】
试题分析: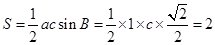 ,所以
,所以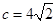 ,由余弦定理得
,由余弦定理得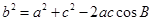
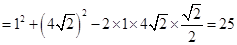 ,因此
,因此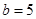 .
.
考点:1.三角形的面积公式;2.余弦定理

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案