题目内容
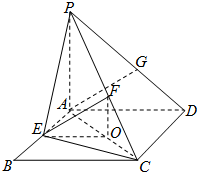
 如图,四边形ABCD为正方形,PA⊥平面ABCD,且AB=4,PA=3,点A在PD上的射影为G点,E点在AB边上,平面PEC⊥平面PDC.
如图,四边形ABCD为正方形,PA⊥平面ABCD,且AB=4,PA=3,点A在PD上的射影为G点,E点在AB边上,平面PEC⊥平面PDC.(Ⅰ)求证:AG∥平面PEC;
(Ⅱ)求BE的长;
(Ⅲ)求直线AG与平面PCA所成角的余弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)作EF⊥PC于F得到EF∥AG,利用线面平行得判定定理可证;
(Ⅱ)由(Ⅰ)知A、E、F、G四点共面,又AE∥CD,容易判断四边形AEFG为平行四边形,利用平行线分线段成比例可求BE;
(Ⅲ))∵EF∥AG,所以AG与平面PAC所成角等于EF与平面PAC所成的角,过E作EO⊥AC于O点,易知EO⊥平面PAC,又EF⊥PC,得到∠EFO即为EF与平面PAC所成的角,然后计算求之.
(Ⅱ)由(Ⅰ)知A、E、F、G四点共面,又AE∥CD,容易判断四边形AEFG为平行四边形,利用平行线分线段成比例可求BE;
(Ⅲ))∵EF∥AG,所以AG与平面PAC所成角等于EF与平面PAC所成的角,过E作EO⊥AC于O点,易知EO⊥平面PAC,又EF⊥PC,得到∠EFO即为EF与平面PAC所成的角,然后计算求之.
解答:
 (Ⅰ)证明:∵CD⊥AD,CD⊥PA
(Ⅰ)证明:∵CD⊥AD,CD⊥PA
∴CD⊥平面PAD∴CD⊥AG,
又PD⊥AG
∴AG⊥平面PCD …(2分)
作EF⊥PC于F,因面PEC⊥面PCD
∴EF⊥平面PCD
∴EF∥AG,又AG?面PEC,EF?面PEC,
∴AG∥平面PEC …(3分)
(Ⅱ)由(Ⅰ)知A、E、F、G四点共面,又AE∥CD∴AE∥平面PCD
∴AE∥GF∴四边形AEFG为平行四边形,∴AE=GF …(4分)
∵PA=3,AB=4∴PD=5,AG=
,
又PA2=PG•PD∴PG=
…(5分)
又
=
∴GF=
∴AE=
,
故BE=
…(7分)
(3)∵EF∥AG,所以AG与平面PAC所成角等于EF与平面PAC所成的角,过E作EO⊥AC于O点,易知EO⊥平面PAC,又EF⊥PC,
∴OF是EF在平面PAC内的射影
∴∠EFO即为EF与平面PAC所成的角 …(9分)
EO=AEsin45°=
×
=
,又EF=AG=
,
∴sin∠EFO=
=
×
=
故cos∠EFO=
=
所以AG与平面PAC所成角的余弦值等于
…(12分)
 (Ⅰ)证明:∵CD⊥AD,CD⊥PA
(Ⅰ)证明:∵CD⊥AD,CD⊥PA∴CD⊥平面PAD∴CD⊥AG,
又PD⊥AG
∴AG⊥平面PCD …(2分)
作EF⊥PC于F,因面PEC⊥面PCD
∴EF⊥平面PCD
∴EF∥AG,又AG?面PEC,EF?面PEC,
∴AG∥平面PEC …(3分)
(Ⅱ)由(Ⅰ)知A、E、F、G四点共面,又AE∥CD∴AE∥平面PCD
∴AE∥GF∴四边形AEFG为平行四边形,∴AE=GF …(4分)
∵PA=3,AB=4∴PD=5,AG=
| 12 |
| 5 |
又PA2=PG•PD∴PG=
| 9 |
| 5 |
又
| GF |
| CD |
| PG |
| PD |
∴GF=
| 36 |
| 25 |
∴AE=
| 36 |
| 25 |
故BE=
| 64 |
| 25 |
(3)∵EF∥AG,所以AG与平面PAC所成角等于EF与平面PAC所成的角,过E作EO⊥AC于O点,易知EO⊥平面PAC,又EF⊥PC,
∴OF是EF在平面PAC内的射影
∴∠EFO即为EF与平面PAC所成的角 …(9分)
EO=AEsin45°=
| 36 |
| 25 |
| ||
| 2 |
18
| ||
| 25 |
| 12 |
| 5 |
∴sin∠EFO=
| EO |
| EF |
18
| ||
| 25 |
| 5 |
| 12 |
3
| ||
| 10 |
故cos∠EFO=
| 1-sin2∠EFO |
| ||
| 10 |
所以AG与平面PAC所成角的余弦值等于
| ||
| 10 |
点评:本题考查了线面平行得判定定理和性质定理得运用以及线面角得求法,关键是将所求转化为线线问题解答,属于经常考查得题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知
=(4,3),
=(-5,y),并且
⊥
,则y值为( )
| OA |
| OB |
| OB |
| OA |
A、
| ||
B、
| ||
C、
| ||
D、
|

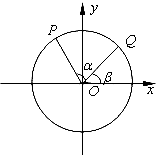 如图,以ox轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P,Q,已知点P的坐标为(-
如图,以ox轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P,Q,已知点P的坐标为(-