题目内容
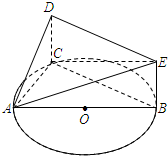 (2013•江门一模)如图,AB是圆O的直径,C是圆O上除A、B外的一点,△AED在平面ABC的投影恰好是△ABC.已知CD=BE,AB=4,tan∠EAB=
(2013•江门一模)如图,AB是圆O的直径,C是圆O上除A、B外的一点,△AED在平面ABC的投影恰好是△ABC.已知CD=BE,AB=4,tan∠EAB=| 1 | 4 |
(1)证明:平面ADE⊥平面ACD;
(2)当三棱锥C-ADE体积最大时,求三棱锥C-ADE的高.
分析:(1)要证两个面相互垂直,可证平面ADE经过平面ACD的一条垂线DE,根据,△AED在平面ABC的投影恰好是△ABC,说明CD和BE都垂直于底面ABC,又CD=BE,可证DE∥BC,利用线面垂直的判定定理可证BC⊥面ACD,从而使问题得证;
(2)把三棱锥C-ADE体积转化为三棱锥E-ACD的体积,写出体积公式后利用基本不等式求体积最大值,并且得到使体积最大时的多面体A-BEDC的确切形状,然后利用等积法可求三棱锥C-ADE的高.
(2)把三棱锥C-ADE体积转化为三棱锥E-ACD的体积,写出体积公式后利用基本不等式求体积最大值,并且得到使体积最大时的多面体A-BEDC的确切形状,然后利用等积法可求三棱锥C-ADE的高.
解答:(1)证明:因为AB是直径,所以BC⊥AC,因为△ABC是△AED的投影,所以CD⊥平面ABC,则CD⊥BC,
因为CD∩AC=C,所以BC⊥平面ACD,
因为CD⊥平面ABC,BE⊥平面ABC,所以CD∥BE,又因为CD=BE,所以BCDE是平行四边形,
∴BC∥DE,则DE⊥平面ACD,因为DE?平面ADE,所以平面ADE⊥平面ACD;
(2)在直角三角形AEB中,EB=AB•tan∠EAB=4×
=1,
由(1)知VC-ADE=VE-ACD=
S△ACD•DE
=
×
AC•CD•DE=
AC•EB•BC=
AC•BC≤
×(AC2+BC2)=
×AB2=
,
等号当且仅当AC=BC=2
时成立,
此时,AD=
=
=3,
S△ADE=
AD•DE=
×3×2
=3
,
设三棱锥C-ADE的高为h,
则VC-ADE=
S△ADE•h=
,
∴
×3
•h=
.
∴h=
.
所以,当三棱锥C-ADE体积最大时,三棱锥C-ADE的高为
.
因为CD∩AC=C,所以BC⊥平面ACD,
因为CD⊥平面ABC,BE⊥平面ABC,所以CD∥BE,又因为CD=BE,所以BCDE是平行四边形,
∴BC∥DE,则DE⊥平面ACD,因为DE?平面ADE,所以平面ADE⊥平面ACD;
(2)在直角三角形AEB中,EB=AB•tan∠EAB=4×
| 1 |
| 4 |
由(1)知VC-ADE=VE-ACD=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 12 |
| 4 |
| 3 |
等号当且仅当AC=BC=2
| 2 |
此时,AD=
| AC2+CD2 |
12+(2
|
S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
设三棱锥C-ADE的高为h,
则VC-ADE=
| 1 |
| 3 |
| 4 |
| 3 |
∴
| 1 |
| 3 |
| 2 |
| 4 |
| 3 |
∴h=
2
| ||
| 3 |
所以,当三棱锥C-ADE体积最大时,三棱锥C-ADE的高为
2
| ||
| 3 |
点评:本题主要考查了直线与平面垂直的判定和性质,考查空间想象能力、运算能力和推理论证能力,训练了利用基本不等式求最值,求棱锥体积最大时的棱锥的高时,运用了等积法,体现了数学转化思想,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目