题目内容
三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=1,PB=PC=
,则P点到平面ABC的距离为
.
| 2 |
| ||
| 2 |
| ||
| 2 |
分析:根据题意利用等体积计算P点到平面ABC的距离,求出△ABC的面积即可.
解答:解:∵PA、PB、PC两两互相垂直,且PA=1,PB=PC=
,
∴AB=AC=
,BC=2
∴A到BC的距离为
∴△ABC的面积为
×2×
=
设P点到平面ABC的距离为h,则
×
×
×
×1=
×
×h
∴h=
即P点到平面ABC的距离为
故答案为:
| 2 |
∴AB=AC=
| 3 |
∴A到BC的距离为
| 2 |
∴△ABC的面积为
| 1 |
| 2 |
| 2 |
| 2 |
设P点到平面ABC的距离为h,则
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
∴h=
| ||
| 2 |
即P点到平面ABC的距离为
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查点到面的距离,解题的关键是利用等体积法进行求解.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.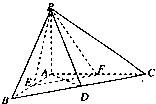 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,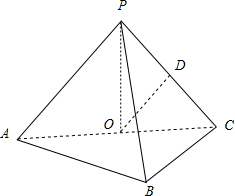 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.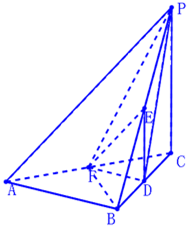 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.