题目内容
8. 《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,下面图表是对这20人血液中酒精含量进行检查所得结果的数据表和频率分布直方图.
| 酒精含量(单位:mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) |
| 人数 | 3 | 4 | x | 1 |
| 酒精含量(单位:mg/100ml) | [60,70) | [70,80) | [80,90) | [90,100] |
| 人数 | y | 3 | m | n |
(注:只需补全[40,50)与[70,80)两段,其他段的已经画好)
(2)从血液酒精浓度在[70,90)范围内的驾驶员中任取3人,求至多有1人属于醉酒驾车的概率.
分析 (1)根据频率直方图的高度可以判断:[50,60)与[90,100]高度相等,可知频数也因该相等,
[60,70)与[80,90)高度相等,可知频数也因该相等,高度为[50,60)的二倍,即可求解各个数段上的频数.画出频率直方图即可.
(2)仔细分析题意得出:因为血液酒精浓度在[70,80)内范围内应抽3人,记为a,b,c,
[80,90)范围内有2人,记为d,e,列举出从中任取2人的所有情况,运用古典概率公式求解即可.
解答  解:(1)根据频率直方图的高度可以判断:[50,60)与[90,100]高度相等,可知频数也因该相等,n=1,
解:(1)根据频率直方图的高度可以判断:[50,60)与[90,100]高度相等,可知频数也因该相等,n=1,
[60,70)与[80,90)高度相等,可知频数也因该相等,m=y,高度为[50,60)的二倍,
所以m=y=2,
x=20-3-4-1-2-3-2-1=20-16=4,
故x=4,y=2,m=2,n=1,
(2)因为血液酒精浓度在[70,80)内范围内应抽3人,记为a,b,c,
[80,90)范围内有2人,记为d,e,则从中任取2人的所有情况为(a,b,c),(a,b,d),(a,b,e),(a,c,d),(a,c,e),(a,d,e),(b,c,d),(b,c,e),(b,d,e),(c,d,e)共10种
至多有一人的血液酒精浓度在[80,90)范围内的情况有(a,b,c),(a,b,d),
(a,b,e),(a,c,d),(a,c,e),(b,c,d),(b,c,e),共7种
设“恰有1人属于醉酒驾车”为事件A,则P(A)=$\frac{7}{10}$.
点评 本题考察了古典概率在实际问题中的应用,考察了学生列举,分析问题的能力,做到不重复,不遗漏.

练习册系列答案
相关题目
16.如图所示的程序框图的运行结果是( )
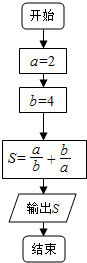

| A. | 2 | B. | 2.5 | C. | 3.5 | D. | 4 |
20.下列说法正确的是( )
| A. | 对于相关系数r来说,|r|≤1,|r|越接近0,相关程度越大;|r|越接近1,相关程度越小 | |
| B. | 对于相关系数r来说,|r|≥1,|r|越接近1,相关程度越大;|r|越大,相关程度越小 | |
| C. | 对于相关系数r来说,|r|≤1,|r|越接近1,相关程度越大;|r|越接近0,相关程度越小 | |
| D. | 对于相关系数r来说,|r|≥1,|r|越接近1,相关程度越小;|r|越大,相关程度越大 |