题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA= acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,求a,c的值.
(1)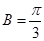 ;(2)
;(2)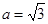 ,
,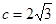 .
.
解析试题分析:(1)由正弦定理 ,可将已知等式bsinA=
,可将已知等式bsinA= acosB化为:
acosB化为: 再注意到sinA
再注意到sinA 0,从而可求得
0,从而可求得 的值,再注意角B的范围就可求出角B的大小;(2)由已知sinC=2sinA及正弦定理可得到c=2a,又因为b=3,由余弦定理
的值,再注意角B的范围就可求出角B的大小;(2)由已知sinC=2sinA及正弦定理可得到c=2a,又因为b=3,由余弦定理 ,结合(1)结果,可得到关于a的一个方程,解此方程可得到a的值,从而得到c的值.
,结合(1)结果,可得到关于a的一个方程,解此方程可得到a的值,从而得到c的值.
试题解析:(1) bsinA=
bsinA= acosB,由正弦定理可得
acosB,由正弦定理可得 , 2分
, 2分
即得 >0,所以
>0,所以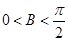 , 4分
, 4分
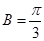 . 5分
. 5分
(2) sinC=2sinA,由正弦定理得
sinC=2sinA,由正弦定理得 , 6分
, 6分
由余弦定理 , 7分
, 7分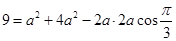 , 8分
, 8分
解得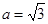 9分
9分
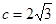 . 10分
. 10分
考点:正弦定理和余弦定理.

练习册系列答案
相关题目
 中,
中, 分别是角
分别是角 的对边,
的对边,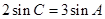 ,
,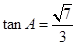 .
.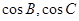 的值; (2)若
的值; (2)若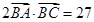 ,求
,求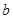 的值.
的值.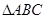 的内角
的内角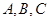 的对边分别
的对边分别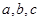 且
且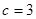 ,
,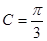 ,若
,若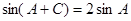 ,求
,求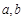 的值。
的值。 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°. ,求PA;
,求PA;

 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小. 的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.
的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.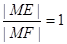 时,试问x的值为多少?(2)求
时,试问x的值为多少?(2)求 的取值范围.
的取值范围. 中,
中, ,那么A=_____________;
,那么A=_____________; 的三个内角
的三个内角 所对的边分别为
所对的边分别为
 ,若
,若 ,
, .
.