题目内容
5.已知函数y=x+$\frac{t}{x}$有如下性质:如果常数t>0,那么该函数在$(0,\sqrt{t}]$上是减函数,在$[\sqrt{t},+∞)$上是增函数.(1)已知f(x)=$\frac{{{x^2}-2x-4}}{x+2}$,x∈[-1,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[-1,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
分析 (1)根据条件,先变形f(x)=$x+2+\frac{4}{x+2}-6$,可令x+2=u,1≤u≤3,而函数u=x+2为增函数,从而根据复合函数的单调性及已知的性质便可得出f(x)的减区间为[-1,0],增区间为[0,1],进一步便可得出f(x)的值域为[-2,-1];
(2)根据题意便知f(x)的值域为g(x)的子集,而容易求出g(x)的值域为[-1-2a,-2a],从而得出$\left\{\begin{array}{l}{-1-2a≤-2}\\{-2a≥-1}\end{array}\right.$,这样即可得出实数a的值.
解答 解:(1)y=$f(x)=\frac{{x}^{2}-2x-4}{x+2}=\frac{(x+2)^{2}-6(x+2)+4}{x+2}$=x+2+$\frac{4}{x+2}$-6;
设u=x+2,x∈[-1,1],1≤u≤3,u=x+2为增函数;
则y=u+$\frac{4}{u}$-6,u∈[1,3];
由已知性质得,①当1≤u≤2,即-1≤x≤0时,f(x)单调递减;
∴f(x)的减区间为[-1,0];
②当2≤u≤3,即0≤x≤1时,f(x)单调递增;
∴f(x)的增区间为[0,1];
由f(-1)=-1,f(0)=-2,f(1)=$-\frac{5}{3}$;
得f(x)的值域为[-2,-1];
(2)g(x)=-x-2a为减函数,x∈[0,1];
故g(x)∈[-1-2a,-2a];
由题意,f(x)的值域是g(x)的值域的子集;
∴$\left\{\begin{array}{l}{-1-2a≤-2}\\{-2a≥-1}\end{array}\right.$;
∴$a=\frac{1}{2}$;
即实数a的值为$\frac{1}{2}$.
点评 考查分离常数法的运用,复合函数的单调性及单调区间的求法,一次函数的单调性,根据函数单调性求函数的值域,以及子集的概念.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (0,1) | B. | (0,2) | C. | (1,2) | D. | (2,3) |
| A. | tanαsinα≥0 | B. | sin2α≤0 | C. | sinα≤0 | D. | cos2α<0 |
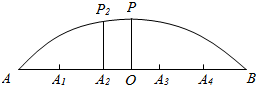 定义区间[a,b]的区间长度为b-a,如图是某圆拱形桥一孔圆拱的示意图.这个圆的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度所处的区间[a,b].(要求区间长度为$\frac{1}{2}$)
定义区间[a,b]的区间长度为b-a,如图是某圆拱形桥一孔圆拱的示意图.这个圆的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度所处的区间[a,b].(要求区间长度为$\frac{1}{2}$) 如图,正方体ABCD-A1B1C1D1棱长为1,P为BC中点,Q为线段CC1上动点,过点A,P,Q的平面截该正方体所得截面记为S.当CQ=$\frac{1}{2}$时,S的面积为$\frac{9}{8}$;若S为五边形,则此时CQ取值范围($\frac{1}{2}$,1).
如图,正方体ABCD-A1B1C1D1棱长为1,P为BC中点,Q为线段CC1上动点,过点A,P,Q的平面截该正方体所得截面记为S.当CQ=$\frac{1}{2}$时,S的面积为$\frac{9}{8}$;若S为五边形,则此时CQ取值范围($\frac{1}{2}$,1).