题目内容
．．(满分8分)已知数列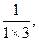
，
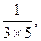
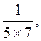
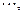
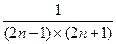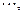
（1）计算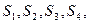
（2）根据（1）的计算结果，猜想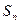
的表达式
，并用数学归纳法进行证明。
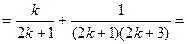
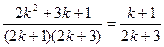
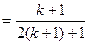
所以，当n=k+1时公式也
成立。
由
①②知，
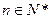时，有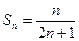
成立。………………………8分
解析
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
云南师大附小一线名师提优作业系列答案冲刺100分单元优化练考卷系列答案题目内容
．．(满分8分)已知数列，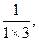
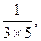
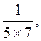
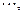
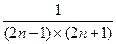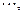
（1）计算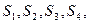
（2）根据（1）的计算结果，猜想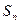的表达式，并用数学归纳法进行证明。
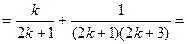
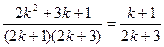
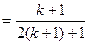
所以，当n=k+1时公式也成立。
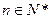由①②知，时，有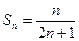成立。………………………8分
解析
云南师大附小一线名师提优作业系列答案冲刺100分单元优化练考卷系列答案
是公差为
的等差数列，
是公比为
的等比数列。
，是否存在
，有
说明理由； 
,
,并说明理由；
试确定所有的
，使数列
。
的导数
；
（
）在区间
上有最大值
和最小值
．设
．
、
的值；
在
上有解，求实数
的取值范围；
有三个不同的实数解，求实数
．
的大致图象；
的零点．