题目内容
已知函数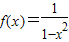 ,
,(1)讨论函数f(x)的性质(定义域,奇偶性,单调性(不要求证明));
(2)根据函数f(x)的性质画出y=f(x)的图象(草图);
(3)判断f(-2-a2)与f(a2+1)(其中a∈R,且a≠0)的大小,并说明理由.
【答案】分析:(1)根据使函数的解析式有意义的原则,可以得到函数的定义域,根据函数奇偶性的定义,可以判断函数的奇偶性,根据复合函数同增异减的原则,可以判断出函数的单调性.
(2)根据(1)中函数的性质,我们易画出y=f(x)的图象(草图);
(3)根据函数的奇偶性,我们可得f(-2-a2)=f(a2+2),再根据函数的单调性,分析两个自变量的大小,即可得到答案.
解答:解:(1)函数f(x)的定义域为:(-∞,-1)∪(-1,1)∪(1,+∞)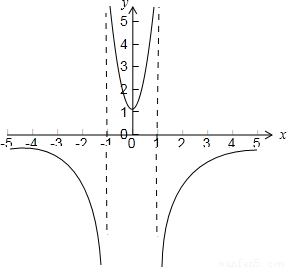
函数f(x)为偶函数,
函数f(x)在区间(-∞,-1),[0,1)上为增函数,
在区间(-1,0],(1,+∞)上为减函数
(2)由(1)中函数的性质,可得y=f(x)的图象如图所示:
(3)∵函数f(x)为偶函数
∴f(-2-a2)=f(a2+2)
又∵f(x)在区间(1,+∞)上为增函数,且a2+2>a2+1≥1
∴f(a2+2)>f(a2+1)
即f(-2-a2)>f(a2+1)
点评:本题考查的知识点是奇偶性与单调性的综合,同时也考查了函数的定义域,图象等,是函数图象和性质的综合考查,熟练掌握基本初等函数的性质和复合函数性质的处理方法,是解答本题的关键.
(2)根据(1)中函数的性质,我们易画出y=f(x)的图象(草图);
(3)根据函数的奇偶性,我们可得f(-2-a2)=f(a2+2),再根据函数的单调性,分析两个自变量的大小,即可得到答案.
解答:解:(1)函数f(x)的定义域为:(-∞,-1)∪(-1,1)∪(1,+∞)

函数f(x)为偶函数,
函数f(x)在区间(-∞,-1),[0,1)上为增函数,
在区间(-1,0],(1,+∞)上为减函数
(2)由(1)中函数的性质,可得y=f(x)的图象如图所示:
(3)∵函数f(x)为偶函数
∴f(-2-a2)=f(a2+2)
又∵f(x)在区间(1,+∞)上为增函数,且a2+2>a2+1≥1
∴f(a2+2)>f(a2+1)
即f(-2-a2)>f(a2+1)
点评:本题考查的知识点是奇偶性与单调性的综合,同时也考查了函数的定义域,图象等,是函数图象和性质的综合考查,熟练掌握基本初等函数的性质和复合函数性质的处理方法,是解答本题的关键.

练习册系列答案
相关题目
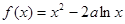 ,
,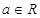
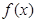 单调区间;
单调区间;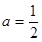 时,证明:当
时,证明:当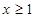 时,证明:
时,证明: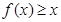 。
。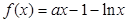
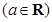 .
.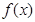 在定义域内的极值点的个数;
在定义域内的极值点的个数; 处取得极值,对
处取得极值,对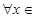
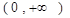 ,
,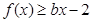 恒成立,求实数
恒成立,求实数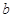 的取值范围.
的取值范围. 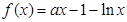
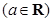 .
.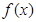 在定义域内的极值点的个数;
在定义域内的极值点的个数;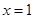 处取得极值,对
处取得极值,对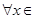
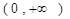 ,
,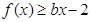 恒成立,求实数
恒成立,求实数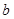 的取值范围;
的取值范围;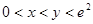 且
且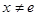 时,试比较
时,试比较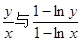 的大小.
的大小. .
. 函数
函数 的单调性;
的单调性; 为偶数时,正项数列
为偶数时,正项数列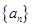 满足
满足 ,求
,求 时,求证:
时,求证: .
. 。(1)讨论函数
。(1)讨论函数 的单调性;(2)当
的单调性;(2)当 时,设
时,设 ,若
,若 时,
时, 恒成立。求整数
恒成立。求整数 的最大值。
的最大值。