题目内容
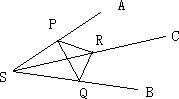
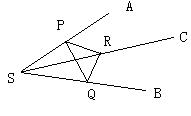
SA、SB、SC是共点于S且不共面的三条射线, 若∠BSC=60°, ∠BSA=∠CSA=45°. 则二面角B-SA-C的大小为________度.
答案:90
解析:
提示:
解析:
|
解: 过SA上一点P, 在平面ASB内作SA的垂线交SB于Q, 在平面ASC内作SA的垂线交SC于R, 则∠QPR即二面角B-SA-C的平面角. 设SP的长度为a, 在Rt△QSP中,
因为 ∠QSR=45°, PQ=PS=a, QS=
同理, PR=PS=a, RS=
在Rt△QSR中, 因为 QS=RS=
所以 QR=
在Rt△QPR中, 因为 PQ=PR=a, QR= 即 PQ2+PR2=QR2, 所以 ∠QPR=90° 所以 二面角B-SA-C等于90°.
|
提示:
| 过SA上的点P, 在面ASB内SA的垂线交SB于Q, 在面ASC内作SA的垂线交SC于R, ∠QPR为所求. |

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目

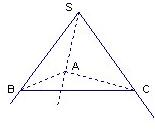 如图,已知SA,SB,SC是由一点S引出的不共面的三条射线,∠ASC=∠ASB=45°,∠BSC=60°,∠SAB=90°,求证:AB⊥SC.
如图,已知SA,SB,SC是由一点S引出的不共面的三条射线,∠ASC=∠ASB=45°,∠BSC=60°,∠SAB=90°,求证:AB⊥SC.