题目内容
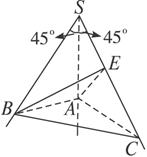
已知SA、SB、SC是共点于S的且不共面的三条射线,∠BSA=∠ASC=45°,∠BSC=60°,求证:平面BSA⊥平面SAC
解析:
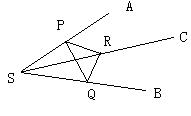
先作二面角B-SA-C的平面角,根据给定的条件,在棱S上取一点P,分别是在两个平面内作直线与棱垂直
证明:在SA上取一点P
过P作PR⊥SA交SC于R
过P作PQ⊥SA交SB于Q
∴∠QPR为二面角B-SA-C的平面角设PS=a
∵∠PSQ=45°,∠SPQ=90°
∴PQ=a,SQ=![]() a
a
同理PR= a,SR= ![]() a
a
∵∠PSQ=60°,SR=SQ=![]() a
a
∴ΔRSQ为正三角形则RQ=![]() a
a
∵PR2+PQ2=2a2=QR2
∴∠QPQ=90°
∴二面角B-SA-C为90°
∴平面BSA⊥平面SAC

练习册系列答案
相关题目
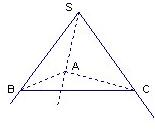 如图,已知SA,SB,SC是由一点S引出的不共面的三条射线,∠ASC=∠ASB=45°,∠BSC=60°,∠SAB=90°,求证:AB⊥SC.
如图,已知SA,SB,SC是由一点S引出的不共面的三条射线,∠ASC=∠ASB=45°,∠BSC=60°,∠SAB=90°,求证:AB⊥SC.