题目内容
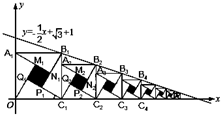 2002年在北京召开的世界数学家大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线y=-
2002年在北京召开的世界数学家大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线y=-| 1 |
| 2 |
| 3 |
分析:利用直角三角形两条直角边的差求出第一个正方形的边长,依次求出第二个、第三个小正方形的边长,归纳总结得到第n个小正方形的边长,则第n个阴影正方形的面积可求.
解答:解:∵每四个全等直角三角形都组成1个大正方形和1个小正方形,把这样的一个组合称为一组.
第一组中,OC1=C1B1,即点B1在直线y=x上,代入直线y=-
x+
+1得,x=y=
(
+1),
∵直角三角形有一个角为30°,可得两直角边OQ1=
(
+1),Q1C1=
(
+1),
小正方形边长为两直角边之差,即为
(
+1)-
(
+1)=
,则小正方形面积为(
)2=
.
∴第1个阴影部分的面积为
.
接下来的每一组大正方形的边长都会逐渐变小,但是成一定规律的.
用前几组做代表,第二组的边长设为x-
(
+1),即为第二组的y值,
代入直线y=-
x+
+1求得x=
(
+1),则第二组大正方形的边长为
(
+1).
第三组的边长设为x-
(
+1),也即为第三组的y值,
代入直线y=-
x+
+1求得x=
(
+1),则第三组大正方形的边长为
(
+1).
如此类推,第n组大正方形的边长为
(
+1).
那么小正方形的边长为(
)n.
∴第n个小正方形的面积为(
)2n.
故答案为:(
)2n.
第一组中,OC1=C1B1,即点B1在直线y=x上,代入直线y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
∵直角三角形有一个角为30°,可得两直角边OQ1=
| 1 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
小正方形边长为两直角边之差,即为
| ||
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
∴第1个阴影部分的面积为
| 4 |
| 9 |
接下来的每一组大正方形的边长都会逐渐变小,但是成一定规律的.
用前几组做代表,第二组的边长设为x-
| 2 |
| 3 |
| 3 |
代入直线y=-
| 1 |
| 2 |
| 3 |
| 10 |
| 9 |
| 3 |
| 6 |
| 9 |
| 3 |
第三组的边长设为x-
| 6 |
| 9 |
| 3 |
代入直线y=-
| 1 |
| 2 |
| 3 |
| 38 |
| 27 |
| 3 |
| 8 |
| 27 |
| 3 |
如此类推,第n组大正方形的边长为
| 2n |
| 3n |
| 3 |
那么小正方形的边长为(
| 2 |
| 3 |
∴第n个小正方形的面积为(
| 2 |
| 3 |
故答案为:(
| 2 |
| 3 |
点评:本题考查了数列的函数特性,考查了数列和求法,解答的关键在于通过求解前几个小正方形的边长,总结出小正方形边长的关于n的函数表达式,是中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
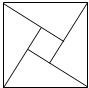 2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos2θ的值等于
2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos2θ的值等于 2002年在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为
2002年在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为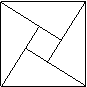
 ,那么
,那么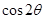 的值等于 .
的值等于 .