题目内容
正三棱锥底面三角形的边长为| 3 |
分析:由正三棱锥的底面边长是
,可以求出底面积和底面△的高;由侧棱长是2,可以求出侧面上的斜高,从而求得三棱锥的高;即得三棱锥的体积.
| 3 |
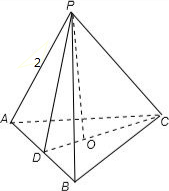
解答:解:如图,在正三棱锥P-ABC中,底面边长AB=
,侧棱长PA=2,
设顶点P在底面的射影为O,连接CO并延长,交AB与点D;
连接PD,则CD⊥AB,PD⊥AB;
在正△ABC中,AB=
,
∴CD=
•AB=
×
=
,
OD=
•CD=
×
=
,
PD=
=
=
,
∴PO=
=
=
,
所以,正三棱锥P-ABC的体积为:
V=
•S△ABC•PO=
×
×(
)2×
=
.
故答案为:
.
| 3 |
设顶点P在底面的射影为O,连接CO并延长,交AB与点D;
连接PD,则CD⊥AB,PD⊥AB;
在正△ABC中,AB=
| 3 |
∴CD=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
OD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
PD=
| PA2-AD2 |
22-(
|
| ||
| 2 |
∴PO=
| PD2-OD2 |
(
|
| 3 |
所以,正三棱锥P-ABC的体积为:
V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 3 |
| 3 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |

点评:本题考查了三棱锥体积公式的应用,关键是求出三棱锥的高;求高时借助空间中垂直关系和勾股定理得出,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
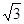 ,侧棱长为2,则其体积为( )
,侧棱长为2,则其体积为( )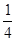 B.
B.
 C.
C.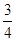 D.
D.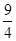
 ,侧棱长为2,则其体积为( )
,侧棱长为2,则其体积为( )


