题目内容
设椭圆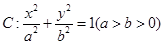 的左、右焦点分别为
的左、右焦点分别为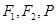 是
是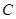 上的点
上的点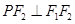 ,
,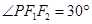 ,则椭圆
,则椭圆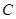 的离心率为( )
的离心率为( )
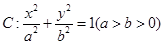 的左、右焦点分别为
的左、右焦点分别为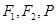 是
是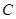 上的点
上的点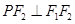 ,
,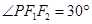 ,则椭圆
,则椭圆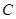 的离心率为( )
的离心率为( )A.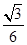 | B.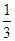 | C.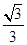 | D.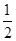 |
C
试题分析:由题意,设
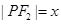 ,则
,则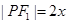 ,
,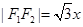 ,所以由椭圆的定义知
,所以由椭圆的定义知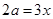 ,又因为
,又因为 ,所以离心率为
,所以离心率为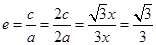 ,故选C.
,故选C.
练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
题目内容
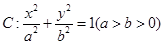 的左、右焦点分别为
的左、右焦点分别为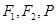 是
是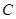 上的点
上的点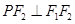 ,
,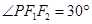 ,则椭圆
,则椭圆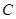 的离心率为( )
的离心率为( )A.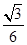 | B.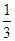 | C.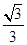 | D.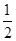 |
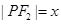 ,则
,则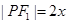 ,
,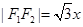 ,所以由椭圆的定义知
,所以由椭圆的定义知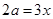 ,又因为
,又因为 ,所以离心率为
,所以离心率为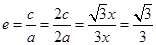 ,故选C.
,故选C.
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案