题目内容
14．在直角坐标系中，函数$f（x）={（\frac{1}{2}）^{|{x+1}|}}$的大致图象为（ ）| A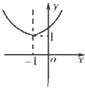． |  | B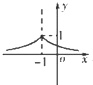． |  | C． |  | D． |  |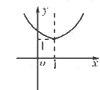
分析 先化为分段函数再根据指数函数的单调性即可判断．
解答 解：数$f（x）={（\frac{1}{2}）^{|{x+1}|}}$=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x+1}，x≥-1}\\{{2}^{x+1}，x＜-1}\end{array}\right.$，
∴当x≥-1时，函数为减函数，当x＜-1时，函数为增函数，
故选：B．
点评 本题考查了指数函数的单调性和分段函数的问题，属于基础题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
2．已知$f（x）=\left\{{\begin{array}{l}{-x（-1＜x＜0）}\\{{x^2}（0≤x＜1）}\\{x（1≤x≤2）}\end{array}}\right.$，求$f（\frac{1}{2}）$=（ ）
| A． | $\frac{1}{4}$ | B． | $-\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $-\frac{1}{4}$ |
9．A为直线3x+4y=10上的一动点，过A作圆x2+y2=1的两条切线，切点分别为P，Q，则四边形OPAQ的面积的最小值是（ ）
| A． | $\sqrt{3}$ | B． | $2\sqrt{3}$ | C． | 2 | D． | 4 |
3．已知函数f（x）=$\sqrt{3}$sinx+acosx的图象的一条对称轴为x=$\frac{π}{3}$．则函数f（x）的单调递增区间为（ ）
| A． | [2kπ-$\frac{2π}{3}$，2kπ+$\frac{π}{3}$]（k∈Z） | B． | [2kπ-$\frac{2π}{3}$，2kπ+$\frac{2π}{3}$]（k∈Z） | ||
| C． | [2kπ-$\frac{π}{3}$，2kπ+$\frac{π}{3}$]（k∈Z） | D． | [2kπ-$\frac{π}{2}$，2kπ+$\frac{π}{2}$]（k∈Z） |
4．已知两直线l1：（a-1）x-3y-10=0，l2：（a+1）x+y+3=0互相平行，则a=（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | -1 |