题目内容
已知无穷数列{an}为等差数列,各项均为正数,给出方程aix2+2ai+1x+ai+2=0(i=1,2,3,…).(1)求证这些方程有一个公共根为-1;
(2)设这些方程除公共根以外的另一根为αi,且f(n)=(α1+1)(α2+1)+(α2+1)(α3+1)+…+(αn+1)(αn+1+1).求证:f(n)<
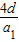 .(其中d为数列{an}的公差)
.(其中d为数列{an}的公差)
【答案】分析:(1)利用等差数列的性质可得ai+ai+2=2ai+1,x=-1代入所给方程可证明;
(2)由韦达定理可得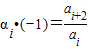 ,由此可得ai,进而可用ai,d表示ai+1,则
,由此可得ai,进而可用ai,d表示ai+1,则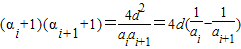 ,用裂项相消法可得f(n),从而可证明;
,用裂项相消法可得f(n),从而可证明;
解答:(1)证明:因为{an}为等差数列,所以ai+ai+2=2ai+1,
将x=-1代入所给方程,得ai-2ai+1+ai+2=0(i=1,2,3,…).
所以这些方程有一个公共根为-1;
(2)∵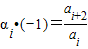 ,∴
,∴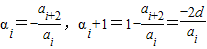 ,
,
∴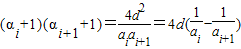 ,
,
∴(α1+1)(α2+1)+(α2+1)(α3+1)+…+(αn+1)(αn+1+1)
=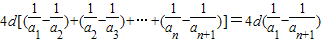 <4d•
<4d•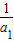 =
=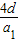 ,即
,即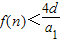 ;
;
点评:本题考查数列与不等式的综合、等差数列的通项公式及数列求和,解决(2)问的关键时化简f(n).
(2)由韦达定理可得
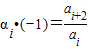 ,由此可得ai,进而可用ai,d表示ai+1,则
,由此可得ai,进而可用ai,d表示ai+1,则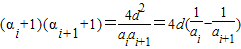 ,用裂项相消法可得f(n),从而可证明;
,用裂项相消法可得f(n),从而可证明;解答:(1)证明:因为{an}为等差数列,所以ai+ai+2=2ai+1,
将x=-1代入所给方程,得ai-2ai+1+ai+2=0(i=1,2,3,…).
所以这些方程有一个公共根为-1;
(2)∵
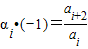 ,∴
,∴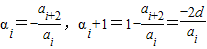 ,
,∴
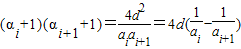 ,
,∴(α1+1)(α2+1)+(α2+1)(α3+1)+…+(αn+1)(αn+1+1)
=
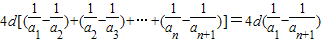 <4d•
<4d•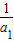 =
=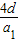 ,即
,即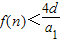 ;
;点评:本题考查数列与不等式的综合、等差数列的通项公式及数列求和,解决(2)问的关键时化简f(n).

练习册系列答案
相关题目