题目内容
过点A(3,-2),且与两轴围成的三角形面积为10,则这样的直线有________条.
2
分析:设所求的直线方程为y=kx-3k-2,(k≠0),直线与两坐标轴的交点坐标是(0,-3k-2,),(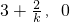 ).当k>0时,
).当k>0时,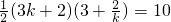 ,整理,得9k2-8k+4=0,△=64-144<0,k不存在.当k<0时,
,整理,得9k2-8k+4=0,△=64-144<0,k不存在.当k<0时,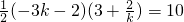 ,或
,或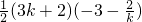 =10,
=10,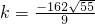 .满足条件的直线有2条.
.满足条件的直线有2条.
解答:设所求的直线方程为y=kx-3k-2,(k≠0),
直线与两坐标轴的交点坐标是(0,-3k-2,),(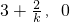 )
)
当k>0时,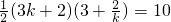 ,
,
整理,得9k2-8k+4=0,
∵△=64-144<0,
∴k不存在.
当k<0时,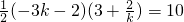 ,或
,或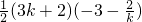 =10,
=10,
当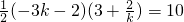 时,
时,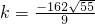 .
.
当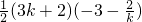 =10时,
=10时,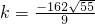 .
.
∴满足条件的直线有2条.
故答案为:2.
点评:本题考查直线的截距式方程,解题时要认真审题,注意距离和截距的区别.
分析:设所求的直线方程为y=kx-3k-2,(k≠0),直线与两坐标轴的交点坐标是(0,-3k-2,),(
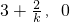 ).当k>0时,
).当k>0时,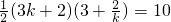 ,整理,得9k2-8k+4=0,△=64-144<0,k不存在.当k<0时,
,整理,得9k2-8k+4=0,△=64-144<0,k不存在.当k<0时,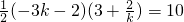 ,或
,或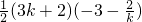 =10,
=10,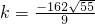 .满足条件的直线有2条.
.满足条件的直线有2条.解答:设所求的直线方程为y=kx-3k-2,(k≠0),
直线与两坐标轴的交点坐标是(0,-3k-2,),(
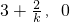 )
)当k>0时,
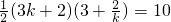 ,
,整理,得9k2-8k+4=0,
∵△=64-144<0,
∴k不存在.
当k<0时,
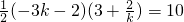 ,或
,或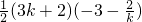 =10,
=10,当
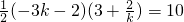 时,
时,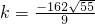 .
.当
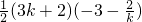 =10时,
=10时,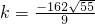 .
.∴满足条件的直线有2条.
故答案为:2.
点评:本题考查直线的截距式方程,解题时要认真审题,注意距离和截距的区别.

练习册系列答案
相关题目