题目内容
设二次函数同时满足下列三个条件.
(1)对称轴为x=-2;
(2)最小值为-9;
(3)二次函数图象与坐标轴有三个交点,且横坐标的积为-5,求二次函数的解析式.
(1)对称轴为x=-2;
(2)最小值为-9;
(3)二次函数图象与坐标轴有三个交点,且横坐标的积为-5,求二次函数的解析式.
分析:由二次函数的性质推出,函数在x=-2时取得最小值-9,可设解析式为:y=a(x+2)2-9,又二次函数图象与坐标轴有三个交点,且横坐标的积为-5,可求出a,所以可求出解析式.
解答:解:∵二次函数同时满足(1)对称轴为x=-2;(2)最小值为-9;
所以二次函数的顶点为(-2,-9),
可设解析式为:y=a(x+2)2-9,a>0.
又二次函数图象与坐标轴有三个交点,且横坐标的积为-5,
∴0=a(x+2)2-9,
即ax2+4ax+4a2-9=0,x1+x2=x1•x2=
=-5,解得a=
,a=-1(舍去)
当a=
,满足二次函数图象与坐标轴有三个交点.
∴函数的解析式为:y=
(x+2)2-9.
所以二次函数的顶点为(-2,-9),
可设解析式为:y=a(x+2)2-9,a>0.
又二次函数图象与坐标轴有三个交点,且横坐标的积为-5,
∴0=a(x+2)2-9,
即ax2+4ax+4a2-9=0,x1+x2=x1•x2=
| 4a2-9 |
| a |
| 9 |
| 4 |
当a=
| 9 |
| 4 |
∴函数的解析式为:y=
| 9 |
| 4 |
点评:本题考查了二次函数的最值及待定系数法求解析式,难度一般,关键算出a的值.

练习册系列答案
相关题目
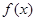 同时满足如下三个条件,求
同时满足如下三个条件,求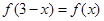 ;②
;②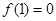 ;③对任意实数
;③对任意实数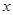 ,都有
,都有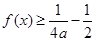 恒成立.
恒成立.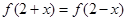 ,(2)被
,(2)被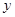 轴截距为6,求此函数解析式
轴截距为6,求此函数解析式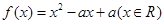 同时满足:
同时满足: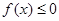 的解集有且只有一个元素;
的解集有且只有一个元素;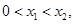 使得不等式
使得不等式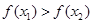 成立.
成立.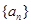 的前
的前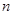 项和
项和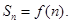
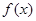 表达式;
表达式;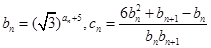 ,
,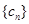 的前
的前 ,
,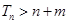 对
对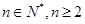
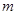 的取值范围.
的取值范围.