题目内容
设对于任意实数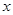 ,不等式
,不等式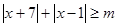 恒成立.
恒成立.
(1)求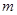 的取值范围;
的取值范围;
(2)当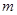 取最大值时,解关于
取最大值时,解关于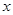 的不等式:
的不等式: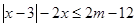 .
.
【答案】
(1)m≤8.(2)原不等式的解集为{x|x≥-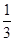 }.
}.
【解析】
试题分析:(1)要使不等式|x+7|+|x-1|≥m恒成立,需f(x)=|x+7|+|x-1|的最小值大于或等于m,问题转化为求f(x)的最小值.
(2)当m取最大值8时,原不等式等价于:|x-3|-2x≤4,去掉绝对值符号,解此不等式.解:(1)设f(x)=|x+7|+|x-1|,则有f(x)=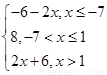
当x≤-7时,f(x)有最小值8;当-7≤x≤1时,f(x)有最小值8;
当x≥1时,f(x)有最小值8.综上f(x)有最小值8,所以,m≤8.
(2)当m取最大值时m=8,原不等式等价于:|x-3|-2x≤4,
等价于:x≥3,且x-3-2x≤4,或x≤3,3-x-2x≤4等价于:x≥3或-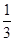 ≤x≤3,
≤x≤3,
所以原不等式的解集为{x|x≥-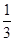 }.
}.
考点:绝对值不等式
点评:本题考查绝对值不等式的解法,以及恒成立问题,体现了等价转化的数学思想.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 成立.
成立. ,如果f(0)=1,判断g(x)=0是否有负实根并说明理由;
,如果f(0)=1,判断g(x)=0是否有负实根并说明理由; 成立.
成立.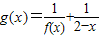 ,如果f(0)=1,判断g(x)=0是否有负实根并说明理由;
,如果f(0)=1,判断g(x)=0是否有负实根并说明理由; 成立.
成立. ,如果f(0)=1,判断g(x)=0是否有负实根并说明理由;
,如果f(0)=1,判断g(x)=0是否有负实根并说明理由;