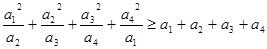题目内容
设
 ,
,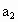 ,
,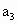 ,
,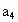 为正数,求证:
为正数,求证: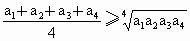 ,并且当且仅当
,并且当且仅当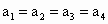 时,等号成立.
时,等号成立.
答案:略
解析:
解析:
|
证明:如果 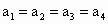 ,则上式左边= ,则上式左边=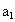 ,右边= ,右边=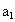 ,故所需要证明的等号成立. ,故所需要证明的等号成立.
如果 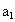 , ,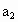 , ,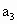 , ,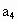 不全相等,则不妨设 不全相等,则不妨设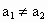 ,于是 ,于是
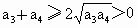 , ,
故有 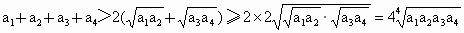 .即 .即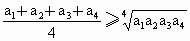 成立. 成立. |

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
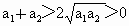
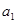 ,
,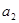 ,
,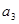 ,
,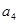 为正数,求证:
为正数,求证: