题目内容
下列说法正确的是
- A.
 ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥
- B.起点相同的两个非零向量不平行
- C.若|
 |=|
|=| |+|
|+| |,则
|,则 与
与 必共线
必共线 - D.若
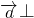
 ,则
,则 与
与 的方向相同或相反
的方向相同或相反
C
分析:根据零向量的性质,我们易判断A的真假,根据平行(共线)向量的性质,我们易判断B,C,D的真假,进而得到答案.
解答:当 =
= 时,
时, ∥
∥ ,
, ∥
∥ ,但
,但 ∥
∥ 不一定成立,故A错误;
不一定成立,故A错误;
起点相同的两个非零向量当他们的方向相同或相反时,一定共线(平行),故B错误;
若| |=|
|=| |+|
|+| |,则
|,则 与
与 同向,即
同向,即 与
与 必共线,故C正确.
必共线,故C正确.
若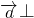
 ,则
,则 与
与 的夹角为90°,故D错误
的夹角为90°,故D错误
故选C
点评:本题考查的知识点是向量加减混合运算及其几何意义,其中熟练掌握向量的基本概念,特别是平行(共线)的定义及性质是解答本题的关键.
分析:根据零向量的性质,我们易判断A的真假,根据平行(共线)向量的性质,我们易判断B,C,D的真假,进而得到答案.
解答:当
 =
= 时,
时, ∥
∥ ,
, ∥
∥ ,但
,但 ∥
∥ 不一定成立,故A错误;
不一定成立,故A错误;起点相同的两个非零向量当他们的方向相同或相反时,一定共线(平行),故B错误;
若|
 |=|
|=| |+|
|+| |,则
|,则 与
与 同向,即
同向,即 与
与 必共线,故C正确.
必共线,故C正确.若
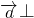
 ,则
,则 与
与 的夹角为90°,故D错误
的夹角为90°,故D错误故选C
点评:本题考查的知识点是向量加减混合运算及其几何意义,其中熟练掌握向量的基本概念,特别是平行(共线)的定义及性质是解答本题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 ,则下列说法正确的是( )
,则下列说法正确的是( ) 有且只有一个零点
B.
有且只有一个零点
B. ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
 ,乙比甲成绩稳定,应该选乙参加比赛
,乙比甲成绩稳定,应该选乙参加比赛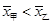 ,甲比乙成绩稳定,应该选甲参加比赛
,甲比乙成绩稳定,应该选甲参加比赛 :函数
:函数 (
( 且
且 )的图像恒过点
)的图像恒过点 ;
; :函数
:函数 有两个零点.
有两个零点.  为假命题 D.
为假命题 D. 为真命题
为真命题 的导函数
的导函数 的图象如上图所示,则下列说法正确的是 ( )
的图象如上图所示,则下列说法正确的是 ( ) 内单调递减 B、函数
内单调递减 B、函数 内单调递增
内单调递增 处取极大值 D、函数
处取极大值 D、函数 处取极小值
处取极小值