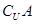题目内容
设集合U是全集,A⊆U,B⊆U,则“A∪B=U”是“B=∁UA”的 条件.
【答案】分析:假设“B=∁UA”,根据补集的定义,易得“A∪B=U”成立,但“A∪B=U”时,若A∩B≠∅时,B≠∁UA,据此易得到“A∪B=U”⇒“B=∁UA”的真假,根据充要条件的定义,易得到答案.
解答:解:当A∩B≠∅时,B≠∁UA.
则“A∪B=U”⇒“B=∁UA”为假命题
若“B=∁UA”则“A∪B=U”
故“A∪B=U”是“B=∁UA”的必要不充分条件
故答案为:必要不充分
点评:本题考查的知识点是必要条件、充分条件和充要条件的判断,根据充要条件的定义,先判断A∪B=U”⇒“B=∁UA”,再判断“B=∁UA”⇒“A∪B=U”是解答本题的关键.
解答:解:当A∩B≠∅时,B≠∁UA.
则“A∪B=U”⇒“B=∁UA”为假命题
若“B=∁UA”则“A∪B=U”
故“A∪B=U”是“B=∁UA”的必要不充分条件
故答案为:必要不充分
点评:本题考查的知识点是必要条件、充分条件和充要条件的判断,根据充要条件的定义,先判断A∪B=U”⇒“B=∁UA”,再判断“B=∁UA”⇒“A∪B=U”是解答本题的关键.

练习册系列答案
相关题目
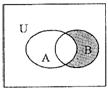
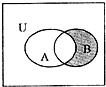 设集合U是全集,若已给的Venn图表示了集合A,B,U之间的关系,则阴影部分表示的集合是( )
设集合U是全集,若已给的Venn图表示了集合A,B,U之间的关系,则阴影部分表示的集合是( )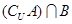 B.
B.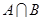
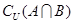 D.
D.