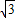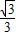题目内容
已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-3,| 3 |
(1)求行列式
|
(2)若函数f(x)=cos(x+α)cosα+sin(x+α)sinα(x∈R),
求函数y=
| 3 |
| π |
| 2 |
分析:(1)利用行列式的运算法则,展开
化简,通过任意角的三角函数求出sinα,cosα代入求得它的值;
(2)函数f(x)=cos(x+α)cosα+sin(x+α)sinα(x∈R),化为f(x)=cosx,然后代入函数y=
f(
-2x)+cos2x+1,利用两角和的正弦函数化为y=2sin(2x+
)+1,直接求出它的最大值,并指出取到最大值时x的值.
|
(2)函数f(x)=cos(x+α)cosα+sin(x+α)sinα(x∈R),化为f(x)=cosx,然后代入函数y=
| 3 |
| π |
| 2 |
| π |
| 6 |
解答:解:(1)因为角α终边经过点P(-3,
),
所以sinα=
,cosα=-
,tanα=-
,
=sinαcosα-tanα=-
+
=
;
(2)f(x)=cos(x+α)cosα+sin(x+α)sinα=cosx(x∈R)函数y=
cos(
-2x)+1+cos2x=
sin2x+1+cos2x
=2sin(2x+
)+1
ymax=3,此时x=kπ+
(k∈Z)
| 3 |
所以sinα=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
|
| ||
| 4 |
| ||
| 3 |
| ||
| 12 |
(2)f(x)=cos(x+α)cosα+sin(x+α)sinα=cosx(x∈R)函数y=
| 3 |
| π |
| 2 |
| 3 |
=2sin(2x+
| π |
| 6 |
ymax=3,此时x=kπ+
| π |
| 6 |
点评:本题是基础题,考查三角函数的化简求值,两角和的正弦函数的应用、二倍角的应用,行列式的计算法则,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ),且2α∈[0,2π),则tanα等于( )
),且2α∈[0,2π),则tanα等于( )



 ),且2α∈[0,2π),则tanα等于( )
),且2α∈[0,2π),则tanα等于( )